Целью этой статьи является нахождение закона изменения температуры твердого тела под действием β-излучения.
Как мы знаем ионизирующее излучение очень силньно влияет на твердые тела, меняя их структуры, вызывая повышение температуры и т.д.
Твердое тело под действием β-излучения
Представим себе твердое тело ноходяшееся в радиационном поле бетта излучения. Чтобы упростить задачу представим твердое тело в виде параллелипипеда, а β-излучение идет по горизонтальному направлению, перпендекулярно стенкам параллелипипеда. Предположим, что β частицы не отражаются от стенок твердого тела, то есть полностью поглощаются. И энергия излучения передаетя твердому телу полностью.
Введем величину А. А – поток β-излучения, или число частиц приходящтхся на единицу площади, в единицу времени. Тогда число частиц приходящихся на твердое тело в единицу времени равно:
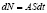 , (1)
, (1)
S – боковая площадь паралелипипеда.
Изменение внутренней энергии сиситемы происходит из-за привода тепла и изменения частиц в системе.
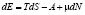 . (2)
. (2)
Если предположить что привода тепла нет, то есть нету теплового контакта с другими телами и нету воздействия электромагнитных волн, также учесть что обьем тела не изменяется то:
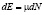 , (3)
, (3)
μ – изменение энергии системы при изменении числа частиц на единицу. Велечину μ называют химическим потенциалом [1, c.68-69].
Фрмулу (3) под ставим в формулу (1). Тогда:
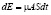 . (4)
. (4)
Каждая β-частица обладает кинетической энергией. Ввиду малой потенциальной энергии, потенциальную энергию β-частиц не учитываем. Значит полная энергия β-частицы равна ее кинетическойэнергии Wk. Отсюда следует:
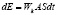 . (5)
. (5)
Как мы знаем, твердое тело состоит из кристаллической решетки. Около кристаллической решетки находятся электроны и они колеблются около положения равновесия. Температура твердого тела характерезуется колебанием кристаллической решетки и электронов в твердом теле. Внутренняя энергия твердого тела складывается из энергии кристаллической решетки и энергии электронов.
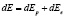 , (6)
, (6)
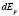 – энергия кристалической решетки,
– энергия кристалической решетки, 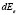 – энергия электронов.
– энергия электронов.
Зависимость температуры от времени в области низкой температуры
Есть такая величина как температура Дебая. При этой температуре в твердом теле возбуждается весь спектр нормальных колебаний, включая и колебание с максимальной частатой ωд.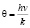 – дебаевская температура.
– дебаевская температура.
Температуры T>q называются высокими. Температуры T<<q называются низкими температурами [1, c. 89-93]. Расссмотрим изменение температуры твердого тела от β-излучения в области низких температур, T<<q.
Энергия кристаллической решетки и электронов в этой области:
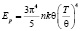 ,
, 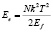 , (7)
, (7)
N – число электронов; n – число атомов в кристаллической решетке; Ef – энергия Ферми. Энергия Ферми – энергия, при которой вероятность заполнения равняется 0,5 [1, с.78].
Энергия решетки изменяется из-за того что β частицы отдают им свою энергию. Число атомов в решетке остается постоянным. по мере прихода все большого количества энергии, атомы будут все больше колебаться, значит температура будет расти.
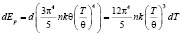 . (8)
. (8)
Энергия электронов будет изменяться из-за повышения температуры, также из-за изменения числа самих электронов.
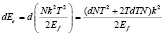 . (9)
. (9)
В формулу (6) подставляем формулу (8) и (9):
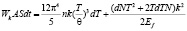 (10)
(10)
dN – изменение числа электронов.
Каждая бетта частица при торможении пораждает несколько пар ионов, следовательно, столько же пар электронов [2, с. 455-457]. Значит изменение электронов равно:
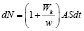 , (11)
, (11)
Wk – начальная энергия β-частицы; w – энергия, необходимая для ионизации одного атома. Величина 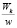 показывает, сколько пар ионов, следовательно и электронов образовалось при полном торможении β-частицы.
показывает, сколько пар ионов, следовательно и электронов образовалось при полном торможении β-частицы.
Раскрывая скобки в формуле (10), вставляя в нее формулу (11), после нескольких преобразований получаем:
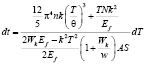 . (12)
. (12)
Формула (12) показывает зависимость изменения температуры твердого тела, находящегося под действием β излучения, в областях низкой температуры, от времени.
Зависимость температуры от времени в области высоких температур
Расссмотрим изменение температуры твердого тела от β-излучения в области высоких температур, T>q.
В областях высокой температуры:
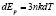 . (13)
. (13)
Энергия электронов остается такой же:
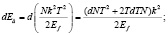
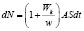 .
.
Проделывая те же операции, что и для области низких температур, получаем:
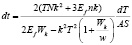 . (14)
. (14)
Эта формула выражает зависимость изменение температуры твердого тела от времени, под воздействием β-излучения, в области высокой температуры.
Заключение
В ходе теоретических исследований были получены две формулы, которые описывают изменение температуры твердого тела, находящегося под действием бетта излучения. Данные формулы описывают изменение температуры твердого тела под воздействием бетта излучение в двух интервалах температур.
Данные формулы могут быть применены в области исследований радиационной безопасности, для расчетов износостойкости специальных покрытий космических аппаратов.

