Введение
Предельные теоремы условно делят на две группы. К первой группе теорем относится закон больших чисел, устанавливающий устойчивость средних значений: при большом числе испытаний их средний результат перестает быть случайным и может быть предсказан с точностью. Вторая группа теорем, которая называется центральной предельной теоремой, она устанавливает условия, благодаря которым закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному.
В данной статье мы рассмотрим неравенство Чебышева, которое используется: а) для грубой оценки вероятностей событий, связанных со случайными величинами, распределение которых неизвестно; б) доказательства ряда теорем закона больших чисел.
Целью данной статьи является успешное изучение и практическое применение теоремы Чебышева и закона больших чисел для эффективной математической подготовки студентов экономических специальностей высших учебных заведений.
Неравенство Чебышева
Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.
Теорема 1. Если случайная величина Х имеет математическое ожидание М(Х)=а и дисперсию D(Х), то для любого ε>0 справедливо неравенство Чебышева.
P {|X–M(X)|}≥ε}≤
(1)
Докажем теорему (1) для непрерывной случайной величины Х с плотностью f(x).
Вероятность
- это вероятность попадания случайной
величины Х в область, лежащую вне промежутка 
.Можно записать
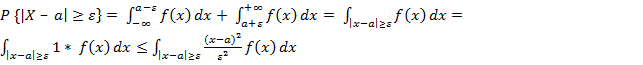
Так как область интегрирования 
можно записать в виде
2 ≥ ε2,откуда следует
. Имеем
,
так как интеграл неотрицательной функции при расширении области интегрирования может только увеличиться. Поэтому
,
Аналогично доказывается неравенство Чебышева и для дискретной случайной величины. Рассмотрим случайную величину Х с математическим ожиданием М(Х) и дисперсией D(X). Тогда теорема, приведенная ниже, является справедливой.
Теорема 2. Вероятность того, что
величина Х отклоняется от своего математического ожидания М(Х) не меньше
любого положительного числа ε
ограничена сверху величиной 
, то есть
P {|X – M(X)|} <ε} ≥ 1-
(2)
В форме (2) оно устанавливает нижнюю границу вероятности события, а в форме (1) – верхнюю.
Неравенство Чебышева справедливо для случайных величин Х= m, имеющей биноминальное распределение с математическим ожиданием М(Х) = а = np и дисперсией D(X) = npq. Данное неравенство принимает вид
P {| m – np | 
(3)
для частости 
события в n независимых испытаниях, в каждом из
которых оно может произойти с вероятностью p=M()=a, дисперсия которых D()=
, неравенство Чебышева имеет вид
P {| 
– p| 
(4)
Неравенство Чебышева имеет ограниченное
значение, так как часто дает грубую и очевидную оценку. Например, если D(X) >ε2 и 
> 1, то 1-> 0; поэтому в данном случае
неравенство Чебышева указывает на то, что вероятность отклонения
неотрицательна, а это и без того тривиально,так как любая вероятность выражается
неотрицательным числом. Это неравенство используется для вывода теоремы
Чебышева.
Теорема Чебышева
Рассмотрим случайную величину Х, в которой закон распределения изменяется от эксперимента к эксперименту. Тогда будем иметь дело с несколькими (n) величинами.
Теорема 3. Если Х1, Х2,
…, Xn независимые случайные величины с
конечными математическими ожиданиями М(Хi), i=
, и дисперсиями D(Хi), i=, ограниченными одним и тем же числом С,
то есть D(Хi) < С, i=, то при возрастании n среднее арифметическое наблюдаемых
значений величин Хi, i=, сходится по вероятности к среднему
арифметическому их ожиданий, то есть для любого ε> 0
(5)
Рассмотрим величинуY=
. Ее математическое ожиданиеM(Y) = 
, а дисперсияD(Y) = 
.
Применим к величине Y неравенство Чебышева, получим
P(
Y – M(Y) 
D(Y)
или
P (
) 
Так как
, то
= 
(6)
Как бы ни было мало 
, переходя к пределу в формуле (6) при n
, получим
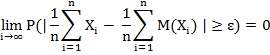
что и требовалось доказать.
Таким образом, теорема Чебышева
утверждает, что среднее арифметическое достаточно большого числа независимых
случайных величин (дисперсии которых равномерно ограниченны) перестает быть
случайной величиной. То есть оно является устойчивым и сходится по вероятности
к определенной неслучайной величине, так как среднее арифметическое
математических ожиданий - величина неслучайная.
Можно получить другую формулировку закона больших чисел, если в формуле (5) перейти к вероятности противоположного события
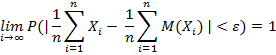
Для одинаково распределенных случайных
величин Хi, i= существует частный случай теоремы
Чебышева.
Теорема 4 (теорема Хинчина). Пусть Х1, Х2, … -
независимые одинаково распределенные случайные величины, которые имеют конечные
математические ожидания М(Хi) = m. Тогда последовательность {Yn}, где Yn
, сходится m с вероятностью 1, то есть для любого ε>0
Закон больших распространяется на зависимые случайные величины.
Теорема 5 (теорема Маркова). Если для случайных величин Х1, Х2, …
= 0
то среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:
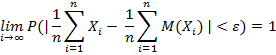
для любого ε> 0
Сущность теоремы Чебышева состоит в том, что отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеяно мало.
Отсюда следует, невозможно с уверенностью предсказать какое вероятное значение примет каждое из случайных величин, но можно предвидеть какое значение примет их среднее арифметическое.
Таким образом, среднее арифметическое достаточно большого числа независимых случайных величин утрачивает характер случайной величины. Это можно объяснить тем, что отклонение каждой их величин от своих математических ожиданий могут быть и положительными, и отрицательными, а в среднем арифметическом они взаимно погашаются.
Теорема Чебышева является справедливой не только для дискретных, но и для непрерывных величин; она представляет собой яркий пример, который подтверждает справедливость учения диалектического материализма о связи между случайностью и необходимостью.