Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Введение

Применение дифференциальных уравнений в математических моделях реальных процессов позволяет решать задачи в различных областях техники, науки, производства. Например, в ядерной физике – при изучении процессов радиоактивного распада веществ. Поэтому в силу компьютеризации очень полезно иметь программу, позволяющую численно решить ОДУ.

Цель исследования

Целью исследования является решение задачи Коши 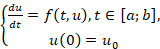(1)

(1)

численными методами – методами Рунге-Кутты второго, третьего и четвёртого порядков аппроксимации.

Материал и методы исследования

Рассмотрим равномерную разностную сетку отрезка :

, где 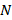– заданное количество равных частей, на которые разбит отрезок , – шаг разбиения.

Пусть 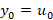, 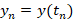. Тогда будут справедливы явные разностные методы Рунге-Кутты [1,2]:

явный двухэтапный метод Рунге-Кутты второго порядка аппроксимации:

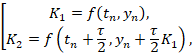
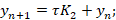
явный трёхэтапный метод Рунге-Кутты третьего порядка аппроксимации:

явный четырёхэтапный метод Рунге-Кутты четвёртого порядка аппроксимации:

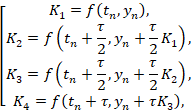
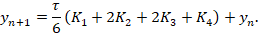
Будет продемонстрирована реализация на языке программирования C++ сформулированных выше методов Рунге-Кутты для решения задачи Коши (1) в случае, когда , а также будет рассмотрена визуализация следа точного решения и визуализация разностного решение задачи Коши (1) в одном окне. Однако эти данные можно несложно быстро поменять и решить задачу Коши (1) с другими данными .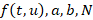

Результаты исследования и их обсуждение

Программный код для решения задачи Коши

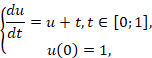
если мелкость разбиения :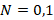

#include <SFML/Graphics.hpp>

#include <cmath>

#include <iostream>

using namespace sf;

using namespace std;

//ширина окна для визуализации решения

const int W = 752;

//высота окна для визуализации решения

const int H = 802;

//следующие данные можно изменить, если необходимо решить другую задачу Коши (1)

const int N = 10;

const double a = 0;

const double b = 1;

const double y_0 = 1; //начальное условие u(0)=1

//объявление функции f(t,u)

double f(double t, double u) {

return t + u;

}

//обявление функции - точного решения задачи Коши (1)

double ExactSolution(double x) {

return 2 * exp(x) - x - 1;

}

int main() {

setlocale(LC_ALL, "Russian");

//tau - мелкость разбиения, T - массив значений равномерной разностной сетки, Y - массив значений разностного решения (1)

double tau = (b - a) / N;

double T[N + 1] = {};

for (int i = 1; i <= N; i++) T[i] = a + i * tau;

double Y[N + 1] = {};

Y[0] = y_0;

//z - условие проверки корректности введённых данных пользователем программы

double z = 0;

while (z == 0) {

cout << "Метод Рунге-Кутта какого порядка аппроксимации Вы хотите использовать для приближённого решения задачи Коши?" << endl << "Нажмите:" << endl << "2, если второго порядка аппроксимации;" << endl << "3, если третего порядка аппроксимации;" << endl << "4, если четвёртого порядка аппроксимации" << endl;

int p;

cin >> p;

if (p == 2)

for (int i = 0; i < N; i++) {

double k1 = f(T[i], Y[i]);

double k2 = f(T[i] + tau / 2, Y[i] + tau / 2 * k1);

Y[i + 1] = Y[i] + tau * k2;

z = 1;

}

else if (p == 3)

for (int i = 0; i < N; i++) {

double k1 = f(T[i], Y[i]);

double k2 = f(T[i] + tau / 2, Y[i] + tau / 2 * k1);

double k3 = f(T[i] + tau, Y[i] - tau * k1 + 2 * tau * k2);

Y[i + 1] = Y[i] + tau / 6 * (k1 + 4 * k2 + k3);

z = 1;

}

else if (p == 4)

for (int i = 0; i < N; i++) {

double k1 = f(T[i], Y[i]);

double k2 = f(T[i] + tau / 2, Y[i] + tau / 2 * k1);

double k3 = f(T[i] + tau / 2, Y[i] + tau / 2 * k2);

double k4 = f(T[i] + tau, Y[i] + tau * k3);

Y[i + 1] = Y[i] + tau / 6 * (k1 + 2 * k2 + 2 * k3 + k4);

z = 1;

}

else {

cout << "Такого варианта нет, повторите попытку" << endl;

}

}

//вывод разностного решения и следа точного решения (1)

cout << "t y_n (разностное решение) u_n (след точного решения)" <<endl;

for (int i = 0; i <= N; i++) cout << T[i] << " " << Y[i] <<" "<< ExactSolution(a+tau*i)<< endl;

//следующий фрагмент программы программы написан для визуализации разностного решения и следа точного решения (1), большая часть кода заимствована в [3]

RenderWindow window(VideoMode(W, H), "Exact (black line) and inexact (blue line) solutions of a differential equation");

//центр координатной плоскости

int x0 = W / 2;

int y0 = H / 2;

//ось ox

RectangleShape OsX(Vector2f(W, 1));

OsX.setFillColor(Color::Black);

OsX.setPosition(0, y0);

//ось oy

RectangleShape OsY(Vector2f(1, H));

OsY.setFillColor(Color::Black);

OsY.setPosition(x0, 0);

//стрелки на осях

RectangleShape strel[4];

for (int i = 0; i < 4; i++) {

strel[i].setSize(Vector2f(1, 25));

strel[i].setFillColor(Color::Black);

if (i < 2)

strel[i].setPosition(x0, 0);

else

strel[i].setPosition(W, y0);

}

strel[0].setRotation(25);

strel[1].setRotation(-25);

strel[2].setRotation(60);

strel[3].setRotation(-250);

//выполнение действий, когда открыто окно

while (window.isOpen())

{

Event event;

//закрытие окна - нажать на крестик

while (window.pollEvent(event))

{

if (event.type == Event::Closed)

window.close();

}

//вид окна: белый экран

window.clear(Color::White);

//изображение в окне стрелок

window.draw(OsX);

window.draw(OsY);

for (int i = 0; i < 4; i++)

window.draw(strel[i]);

//масштабирование графика по оси ox

int scalex = 100;

//масштабирование графика по оси oy

int scaley = 100;

//визуализация разностного решения задачи Коши (1)

//синие точки радиуса 2 для визуализации разностного решения (1)

CircleShape point1(2.f);

point1.setFillColor(Color::Blue);

for (int i = 0; i <= N; i++) {

float x = T[i];

float y = Y[i]; // наш график

//меняем ориентацию системы координат, т.к. по опциям окна она не является "стандартной"

float x1 = x0 + x * scalex;

float y1 = y0 - y * scaley;

//выводим на экран разностное решение задачи Коши(1)

point1.setPosition(x1, y1);

window.draw(point1);

}

//визуализация следа точного решения задачи Коши (1)

//чёрные точки радиуса 1 для визуализации следа точного решения (1)

CircleShape point2(1.f);

point2.setFillColor(Color::Black);

float c = 1000;

int mass = (b - a) * c + 1;

for (int i = 0; i < mass; i++) {

float x = a + i / c;

float y = ExactSolution(x);

float x1 = x0 + x * scalex;

float y1 = y0 - y * scaley;

point2.setPosition(x1, y1);

window.draw(point2);

}

window.display();

}

return 0;

}

В результате выполнения программы, если пользователь сначала ошибётся и на вопрос о выборе метода Рунге-Кутты нажмёт 0, а затем исправится и выберет третий порядок аппроксимации будет выведено два окна (рис. 1 и рис. 2).

Рис. 1.

Рис. 2.

Заключение

Таким образом, в работе продемонстрирована программа, реализованная на языке программирования C++ для решения задачи Коши (1). Данный результат можно использовать для сравнения точности методов Рунге-Кутты второго, третьего и четвёртого порядков аппроксимации опытным путём, а также применять в различных областях техники, науки, производства.