Зубчатые передачи являются наиболее распространёнными типами механических передач. Они широко используются в различных отраслях промышленного производства. Сфера их применения настолько обширна, что редкий прибор, механизм или агрегат, использующий в работе вращательное движение, не имеет в своем составе того или иного вида зубчатого подвижного соединения. Цилиндрическая зубчатая передача используется, например, в станкостроении, буровом, металлургическом, горнодобывающем производстве и других видах промышленности [2].
Встречаются зубчатые передачи с эвольвентным зацеплением, зацеплением Новикова и циклоидальным зацеплением. Также профессором Д.Т. Бабичевым в настоящее время разрабатывается усовершенствованный профиль зуба – равнопрочный [6].
Зубчатые передачи работают в условиях больших нагрузок, особенно ударного воздействия многократно повторяющихся нагрузок. Эти нагрузки вызывают усталость материала зубьев, что приводит к разрушению зубьев.
Самый опасный вид разрушения – поломка зуба. Этот вид разрушения зубьев полностью выводит передачу из строя. Чаще поломка наблюдается у основания зуба вследствие периодического действия переменной нагрузки, имеющей отнулевой, пульсирующий характер, а также в результате значительной кратковременной перегрузки (ударной нагрузки). Если зуб работает одной стороной, то первоначальная трещина, как правило, образуется в зоне растяжения. Трещина распространяется вдоль основания зуба, а иногда к его вершине или по какой-то рабочей части зуба [2].
Излом зуба может привести к весьма тяжким последствиям вплоть до разрушения валов и подшипников, а иногда и всего механизма. Для предупреждения излома проводится расчёт зуба по напряжениям изгиба. За поломку отвечают изгибные напряжения. Их можно вычислить по ГОСТ. Существуют методики расчета изгибной прочности зуба. Но для расчета новых профилей зуба, а также для учета влияния подрезания зуба на его изгибную прочность целесообразнее воспользоваться методами анализа [5].
Среди таких методов времени наиболее разработаны и применяются в расчетной практике следующие: метод конечных разностей (МКР), метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). МКР основан на замене дифференциальных уравнений соответствующими уравнениями в конечных разностях, записанных на регулярной сетке. Данный метод не получил широкого распространения из-за трудности описания сложных криволинейных контуров деталей. МКЭ – наиболее общий метод численного решения физических задач, описываемых при помощи дифференциальных уравнений в частных производных. С помощью МКЭ решаются задачи движения жидкости по трубам, анализируются колебания систем, решаются задачи электростатики, смазки и теплопроводности. Он применяется для анализа напряжений и деформаций несущих конструкций и деталей практически любой техники. Следует отметить высокую универсальность реализующих МКЭ программных продуктов. МГЭ характеризуется весьма привлекательной особенностью: интегральные уравнения, описывающие модель, записываются не для всей рассматриваемой области, а лишь для ее границы. Это позволяет уменьшить размерность задачи на единицу и, тем самым, сократить время вычислений и объем требуемой памяти. Трудности программной реализации МГЭ, а также невозможность расчета НДС составных тел являются существенными препятствиями его более широкого распространения [3].
Более сложные задачи, включающие контактные взаимодействия между деталями, рассмотрены на примерах моделирования в программном комплексе ANSYS, являющемся наиболее универсальным и широко распространенным конечно-элементным пакетом [1].
Цель статьи – сравнительная оценка изгибной прочности зубьев с эвольвентным контуром и равнопрочным. Рассмотрим задачу оценки изгибных напряжений в зубе зубчатого колеса, имеющего 15 зубьев в препроцессоре ANSYS.
Основы метода конечных элементов. В настоящее время большинство программных продуктов, предназначенных для выполнения самых различных расчетов, содержат хотя бы одну из реализаций МКЭ. Область применения МКЭ очень обширна и охватывает практически все физические задачи, описываемые дифференциальными уравнениями. Эффективность и универсальность МКЭ, обеспечившие его распространение, связаны с рядом преимуществ МКЭ по сравнению с другими численными методами. Наиболее важные преимущества МКЭ заключаются в следующем.
МКЭ применим к телам, составленным из нескольких материалов.
Криволинейная область исследуемой непрерывной величины может быть аппроксимирована с помощью прямолинейных элементов или описана точно с помощью криволинейных элементов. В результате любая сложность геометрической формы границ исследуемого тела не является препятствием для применения МКЭ.
Варьируя размерами элементов, в исследуемой области легко локализуются зоны, в которых необходимо получить информацию с наибольшей точностью.
При решении конкретных задач, учитываются смешанные граничные условия [3].
Построение модели. Первым шагом реализации МКЭ при решении конкретной технической задачи является разбиение исследуемой области на подобласти. Однако именно этот шаг до настоящего времени не только не формализован, но и не имеет теоретического обоснования. Формальное или несовершенное разбиение области на подобласти может приводить к ошибочным результатам, даже если остальные этапы реализации метода осуществляются грамотно и выполнены с достаточной точностью. Дискретизация области (тела) включает задание числа, размеров и формы подобластей, которые используются для построения дискретной модели реального тела. Решение задачи, с одной стороны, требует назначения элементов достаточно малых размеров, позволяющих повысить точность результатов расчета, а с другой стороны, применение крупных элементов сокращает объем требуемой оперативной памяти компьютера и время вычислений. При разбиении области необходимо учитывать важность определения результатов в ее локальных зонах. Целесообразно уменьшать размеры элементов в тех зонах области, где ожидаемый результат может очень сильно меняться (вблизи отверстий, выточек, галтелей деталей), и увеличивать размеры элементов там, где ожидаемый результат расчета почти постоянен или мало значим для решаемой задачи в целом [3].
Несмотря на то, что навыки в дискретизации исследуемых тел можно получить только в процессе решения конкретных задач, некоторые общие правила разбиения и нумерации конечных элементов, вытекающие из накопленного опыта использования МКЭ, сформулировать можно. Эти правила и некоторые советы относительно дискретизации объекта исследования будут рассмотрены ниже.
Разбиение исследуемой области на конечные элементы. Независимо от решаемой задачи, в процессе дискретизации тела на конечные элементы реализуются две процедуры. Первая заключается в разбиении исследуемого тела (детали) на конечные элементы. Вторая процедура связана с нумерацией элементов и узлов.
При разбиении любой двумерной области на элементы тело сначала делится на четырехугольные или треугольные зоны. Затем эти зоны подразделяются на треугольники. При выполнении последней операции необходимо стремиться к тому, чтобы форма треугольников была, по возможности, близка к равносторонней. В этом случае погрешность МКЭ будет минимальной. МКЭ дает приемлемую точность результатов при отношении длин сторон треугольных элементов не более 1:3.
Границы между зонами должны проходить там, где изменяются геометрия, свойства материала или заданы граничные условия. Равномерное разбиение, при котором все элементы имеют одинаковую форму и размеры, выполнять нецелесообразно, поскольку всегда существует необходимость получения более точных результатов в определенных зонах области, например, в зонах концентрации напряжений. В этих зонах необходима разбивка на более мелкие элементы.
В механике твердого деформируемого тела рассматривается два типа заданных перемещений: узлы перемещаются только в одном направлении (шарнирные опоры) и неподвижные узлы (жесткая заделка). Эти узловые граничные условия учитываются при построении и преобразовании системы уравнений, решение которой позволяет рассчитать неизвестные перемещения в узлах.
Программный комплекс ANSYS. ANSYS – это основанный на методе конечных элементов программный комплекс, предназначенный для автоматизированного инженерного анализа (Computer Aided Engineering – CAE) в таких областях, как механика деформируемого твердого тела, механика жидкости и газа, электромагнетизм, теплопередача, и многих отраслях техники (машиностроение, строительство, транспорт, авиация, космонавтика).
ANSYS является средством, с помощью которого создается CAD-модель конструкции. CAD-моделирование с помощью ANSYS проходит следующие этапы: построение геометрической модели, выбор типа конечных элементов, построение конечно-элементной сетки, задание свойств материалов, выбор типа анализа, приложение нагрузок, задание граничных условий, счет и анализ результатов [1].
Сравнительная оценка изгибной прочности цилиндрических передач. Для проведения сравнительного анализа необходима построить модели эвольвентного зуба и равнопрочного, произвести расчет и сравнить полученные результаты. Алгоритм действий для каждой из моделей одинаков и приведен ниже.
Построение геометрической модели методом снизу-вверх (рисунок 1,2). В первую очередь строятся ключевые точки. Затем, по заданным точкам происходит построение линий. После, по полученным линиям строится поверхность (торцевое сечение зуба). А с помощью выдавливания командой VOFFST получаем трехмерную модель эвольвентного зуба [4].
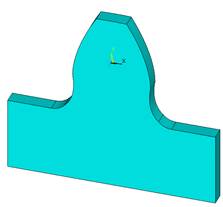
Рисунок 1. Геометрическая модель зуба с эвольвентным профилем
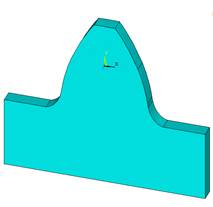
Рисунок 2. Геометрическая модель зуба с равнопрочным профилем
Построение конечно-элементной сетки (рисунок 3,4). Для более точного описания криволинейной поверхности эвольвентного зуба для разбивки был выбран квадратичный элемент SOLID186. Разбивка модели осуществляется элементами размером 1мм. Отдельные элементы, галтели, разбиваются более мелкими элементами, размером 0,2мм. Такая разбивка позволяет получить более точные результаты оценки изгибной прочности зуба.
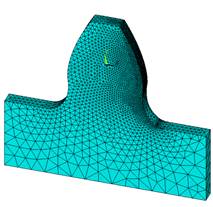
Рисунок 3. Конечно-элементная сетка эвольвентного профиля
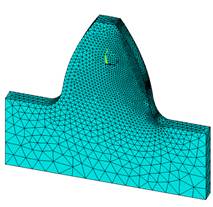
Рисунок 4. Конечно-элементная сетка равнопрочного профиля
Задание граничных условий. Основание зуба жестко заделано. К верхнему ребру головки зуба прикладывается сила 100Н (рисунок 5, 6).
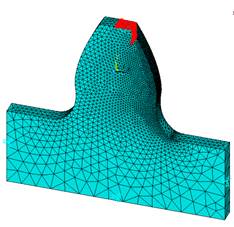
Рисунок 5. Угол приложения силы эвольвентный профиль
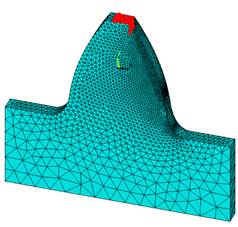
Рисунок 6. Угол приложения силы равнопрочный профиль
Решение поставленной задачи. Для решения задачи в ANSYS по умолчанию используется прямой решатель SPARSE SOLVER [7].
Анализ результатов. Для того, чтобы проанализировать достоверность полученных данных необходимо произвести оценку качества конечно-элементной сетки [4]. Для этого используется следующая формула:
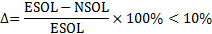
Сетка считается удовлетворительной при Δ<10%. Качество сетки эвольвентного зуба (рисунок 7,8):
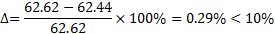
Равнопрочного зуба (рисунок 9,10):
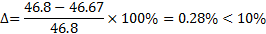
|
|
|
|
|
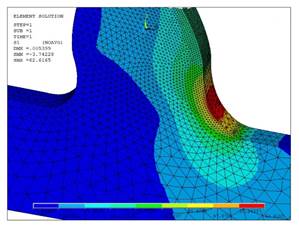
Рисунок 7. Nodal solution эвольвентного профиля |
Рисунок 8. Element solution эвольвентного профиля |
|
|
|
|
|
|
Рисунок 9. Nodal solution равнопрочного профиля |
Рисунок 10. Element solution равнопрочного профиля |
|
Полученные результаты показывают, что в обоих случаях сетка удовлетворительна.
После проведения расчетов осуществляем сравнительную оценку. Для этого сравним суммарные перемещения двух профилей и главные напряжения σ1 растяжения.
Ниже приведены результаты расчетов, представленные в графическом виде.
Суммарные перемещения (рисунок 11, 12). Для эвольвентного зуба суммарные перемещения составили 0,0095, а для равнопрочного – 0,0079. Из этого можно сделать вывод о том, что равнопрочный зуб оказался более устойчив к приложенной силе 100Н.
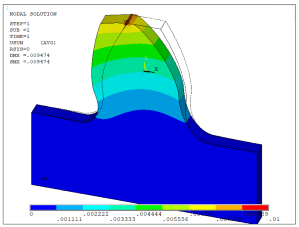
Рисунок 11. Суммарные перемещения эвольвентного профиля
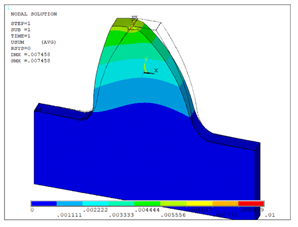
Рисунок 12. Суммарные перемещения равнопрочного профиля
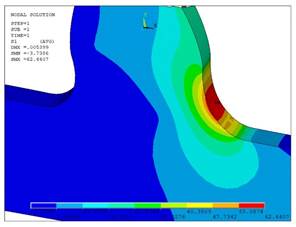
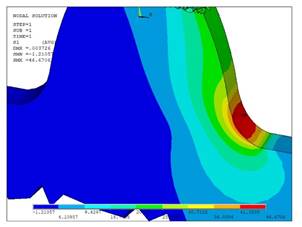
Главные напряжения σ1 – растяжение (рисунок 13, 14). Эвольвентный зуб - 62,44; равнопрочный – 46,67.
Анализируя полученные результаты сравнительной оценки изгибной прочности зубьев цилиндрических передач с эвольвентным контуром и равнопрочным контуром можно сделать вывод о том, что равнопрочный профиль оказался более надежным и устойчивым к приложенным нагрузкам.

Рисунок 13. Главные напряжения σ1 – растяжение эвольвентного профиля

Рисунок 14. Главные напряжения σ1 – растяжение равнопрочного профиля
Библиографическая ссылка
Сызранцева К.В., Бадертдинова А.Ф. СОПОСТАВИТЕЛЬНАЯ ОЦЕНКА ИЗГИБНОЙ ПРОЧНОСТИ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ ПЕРЕДАЧ С ЭВОЛЬВЕНТНЫМ КОНТУРОМ И РАВНОПРОЧНЫМ КОНТУРОМ В ПРОГРАММНОМ КОМПЛЕКСЕ ANSYS // Международный студенческий научный вестник. – 2019. – № 1. ;URL: https://eduherald.ru/ru/article/view?id=19564 (дата обращения: 25.04.2024).