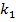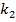В данное время страхование трактуется как сплоченная деятельности страховых компаний, увеличением объемов сделанной работы, уделяет внимание иностранных страховщиков к страховому бизнесу России. Данный процесс осуществляется при возрастании потребности в услугах страховых компаний. В случае если услуги будут падать в плане потребности, то из этого будет следовать закрытие страховых фирм из – за их ненадобности.
На сегодняшний день страхование занимает наивысшее место в экономической отрасли. Так как является приоритетным в экономики России. Основное свойство страхования определяется при помощи формирования денежного фонда и ситуаций, которые приносят потерю видов собственности. Также осуществляется процесс освобождения государственного бюджета от расходов возмещения ущерба.
Главным в страховании является то, что производиться решение социальных проблем общества. Существуют социальные гарантии При предоставлении, которых население получает обеспечение жизни с согласованными возможностями экономики на определенный момент времени.
Все фирмы на данное время можно разделить на две группы, которые не зависят от организационных и правовых форм.
Первая группа проявляется в предоставлении услуг широкого спектра, в которую входят универсальные страховщики. В свою очередь они так же выполняют операции по всем видам перестрахования. Входящие в данную группу страховые компании производят страхование жизни, медицинское страхование, страхование любого вида наземного транспорта.
Страховые общества, которые основываются исключительно на каком то одном виде страхования (общество медицинского страхования) относятся ко второй группе страхования.
Страховые агенты отвечают за успешность работы страховых компаний. В их обязанности входит информирование клиентов о возможных условиях страхования, а так же страховой агент должен исполнить все желания и требования клиента. Следует обратить внимание на то, что страховой агент не числится штатным сотрудником. Заработок страховых агентов напрямую зависит от контрактов. То есть чем больше было заключено контрактов, тем выше процент заработка.
Математический метод так же влияет на успешную работу в данном направлении. Это происходит так же за счет страховых агентов. На основе их деятельности формулируется простой алгоритм модели, который проводит заинтересованность людей воспользоваться услугами страховых компаний.
В связи с тем, что было сказано выше в статье будет рассмотрен математический анализ модели доходной страховой компании, для которой необходимо максимизировать следующее:
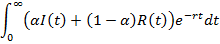
при условии [1]
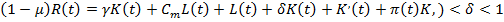
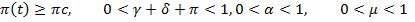

Где 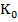 является первоначальным капиталом фирмы, а
является первоначальным капиталом фирмы, а 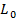 – фонд оплаты труда на начальных условиях. Произведем упрощение действующих значений. Рассуждая [4], что π(t)=
– фонд оплаты труда на начальных условиях. Произведем упрощение действующих значений. Рассуждая [4], что π(t)=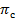 .
.
Не забывая
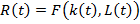 ,
,
и 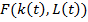 является однотипной [3]. Следуя из этого построим функцию Лагранжа[6]:
является однотипной [3]. Следуя из этого построим функцию Лагранжа[6]:
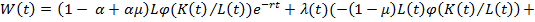
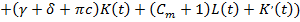 (1)
(1)
В результате [2] первоначальная модель изменит свой вид:
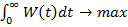 (2)
(2)
при условиях, где [7]
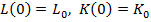 (3)
(3)
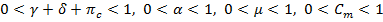 (4)
(4)
Из уравнений (2) – (4) получается система уравнений Эйлера – Лагранжа [5]. Следует выписать ее
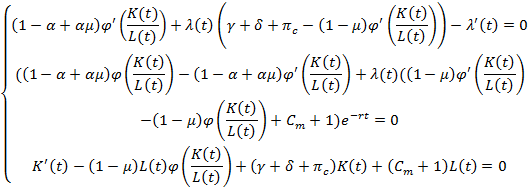
Запишем данную систему в удобном для нас виде [8].
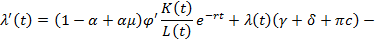
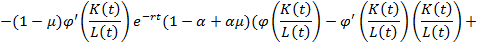
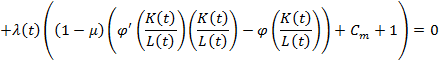
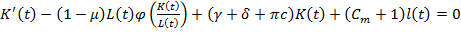 (5)
(5)
Из уравнения (5) сделаем акцент на
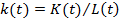
и произведем дифференцирование по t
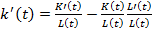 (6)
(6)
Исходя из того, что
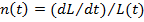
Условия, предоставленные из уравнении (5) получим:
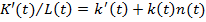 (7)
(7)
Запишем второстепенное обозначение для простоты выражений, которые написаны выше:
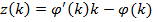 (8)
(8)
Для функции 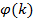 , которая построена [10] на основе
, которая построена [10] на основе 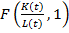 выполняются некоторые условия:
выполняются некоторые условия:
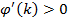
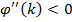
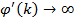 для
для 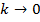
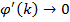 для
для 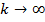
При соблюдении всех обозначений разделим на 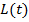 последнее уравнение из (5). Тогда получим:
последнее уравнение из (5). Тогда получим:
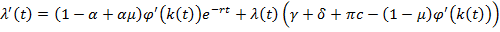 (9)
(9)
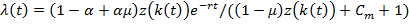 (10)
(10)
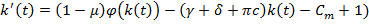 (11)
(11)
Продифференцировав уравнение (10) по t, получим:
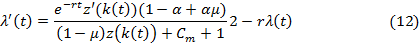
Проверяя то, что
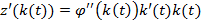 (13),
(13),
Получится то, что формула (12), будет принимать следующий вид [9]
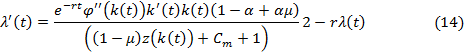
Если в формулу (14) подставлять зависимость (9) и (10), изменяемая скорость капиталовооруженности будет рассчитываться по формуле:
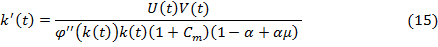
в котором
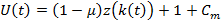
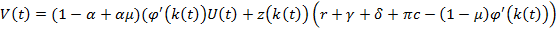
Произведем разбор уравнения (15) .
Следуя из того, что 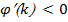 для
для 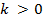 , знаменатель в уравнении (15) является отрицательным. Будем считать, что
, знаменатель в уравнении (15) является отрицательным. Будем считать, что
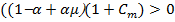 ).
).
Следуя по данному условию на функцию 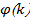 для
для 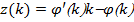 получаем
получаем 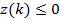 и
и 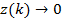 при
при 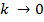 , и
, и 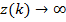 при
при 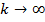 .
.
Для малых k получаем 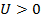 ,
, 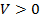 , так как
, так как 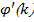 - большое число, соответственно
- большое число, соответственно 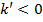 . Если же
. Если же 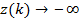 , из этого следует, что
, из этого следует, что 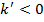 значит для больших
значит для больших 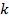 получаем
получаем 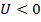 ,
, 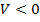 . Из неизменного убывания
. Из неизменного убывания 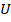 и
и 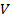 можно сделать заключение, что каждое из рассматриваемых уравнений
можно сделать заключение, что каждое из рассматриваемых уравнений 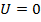 и
и 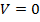 имеет единственный корень.
имеет единственный корень.
Значит область разбивается на три участка: 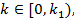
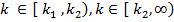
Существует точка не устойчивого равновесия 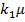 , а так же точки 0 и
, а так же точки 0 и 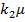 устойчивого равновесия. Нужно обратить внимание, что k1(m) и k2(a,m) монотонно возрастающие функции по m. Если же
устойчивого равновесия. Нужно обратить внимание, что k1(m) и k2(a,m) монотонно возрастающие функции по m. Если же 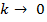 и происходит финансовое разрушение фирмы, то можно сделать вывод, что первоначальное значение
и происходит финансовое разрушение фирмы, то можно сделать вывод, что первоначальное значение 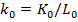 будет меньше чем k1(m). В противном случае размеры фирмы остаются неизменными и возникает стремление к
будет меньше чем k1(m). В противном случае размеры фирмы остаются неизменными и возникает стремление к 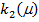 . Из этого следует, что для значений параметров управления
. Из этого следует, что для значений параметров управления 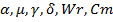
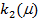 следует воспринимать как преимущественно подходящий размер фирмы. В ходе всех вышеизложенных параметров определяется то, что по существующей величине
следует воспринимать как преимущественно подходящий размер фирмы. В ходе всех вышеизложенных параметров определяется то, что по существующей величине 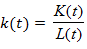 скорей всего будет совершена оценка будущего развития страховой компании и качества первоначального состояния. В ходе этого процесса предлагается следующее:
скорей всего будет совершена оценка будущего развития страховой компании и качества первоначального состояния. В ходе этого процесса предлагается следующее:
Когда 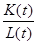 <K(0) из этого следует, что нужно принять меры по росту капитала либо по уменьшению L(t). Если же такая возможность предоставляется то увеличение капитала получается с помощью следующей задачи:
<K(0) из этого следует, что нужно принять меры по росту капитала либо по уменьшению L(t). Если же такая возможность предоставляется то увеличение капитала получается с помощью следующей задачи:
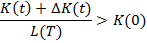
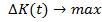
При отсутствии увеличение капитала уменьшается фонд оплаты труда. В таком случае задача приобретет следующий вид:
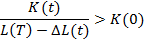
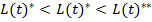
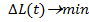
Произведем проверку данного примера, где ранее был сделан расчет оптимального размера фирмы. Необходимо зафиксировать результат изменений параметра управления 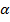 на оптимальный размер страховой компании. Данные для расчета были представлены компанией Росгосстрах. Для того чтобы определить зависимость
на оптимальный размер страховой компании. Данные для расчета были представлены компанией Росгосстрах. Для того чтобы определить зависимость 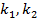 необходимо полагать, что
необходимо полагать, что 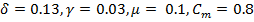 . Данная зависимость отображается в таблице 1.
. Данная зависимость отображается в таблице 1.
Таблица 1. Зависимость k1,k2
|
|
0 |
|
|
|
1 |
|
|
6.8 |
6.8 |
6.8 |
6.8 |
6.8 |
|
|
3.4 |
3.23 |
3.15 |
3.13 |
3 |
Для получения таблицы 2 разрешается разработка значения k1 и k2 для некоторых характеристик, подразумевая то, что m= 0.05.
Таблица 2. Зависимость k1,k2 при 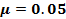
|
|
0 |
|
|
|
1 |
|
|
7.2 |
7.2 |
7.2 |
7.2 |
7.2 |
|
|
3.49 |
3.39 |
3.15 |
3.13 |
2.93 |
В заключении можно сказать, что при изучении капиталовооруженности на норму комиссионного жалованья было обнаружено то, что в данном процессе происходит уменьшение данного изучения, которое может привести к изменению нормы комиссионного жалованья m. При том, K является фиксированным капиталом.
В настоящее время представленное исследование заслуживает усиленного внимания так как при работе страховых компаний имеется неполная причастность страховых агентов.
Представленная в работе модель, может формировать построение некоторых главных проблем приближения условий ее реализации к реальным условиям функционирования страховой компании.
Библиографическая ссылка
Горелова А.Г., Торшина О.А. МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ РОСТА ДОХОДНОЙ СТРАХОВОЙ КОМПАНИИ // Международный студенческий научный вестник. – 2019. – № 1. ;URL: https://eduherald.ru/ru/article/view?id=19528 (дата обращения: 21.11.2024).