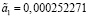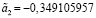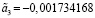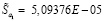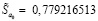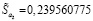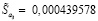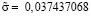К настоящему моменту коммерческие банки развитых стран разработали и протестировали множество математических моделей для оценки кредитного риска заемщиков. Многие из них выдержали проверку временем и сейчас используются в мировой практике. Так, Базельский комитет по банковскому надзору предлагает для оценки кредитного риска стандартный подход, основанный на оценке внешних рейтинговых агентств, и подход на основе внутренних рейтингов [3, C.39–40]. В современных российских условиях, когда большую часть кредитного портфеля банков составляют заемщики, не имеющие рейтингов международных агентств, построить гибкую систему оценки кредитного риска с помощью стандартного подхода достаточно сложно. Именно поэтому для российской банковской системы наиболее актуальными становятся модели оценки кредитного риска на основе внутренних рейтингов банков. В рамках данного подхода банкам необходимо рассчитать одну из ключевых составляющих кредитного риска – вероятность дефолта. Одними из базовых моделей являются модели на основе показателей бухгалтерской и финансовой отчетности. Однако они имеют существенный минус: не позволяют задавать различные макроэкономические сценарии. Решением данной проблемы является корректировка промежуточного показателя дефолта на индекс изменения макроэкономических показателей, который построен на основе регрессионной модели зависимости доли дефолтных компаний от макроэкономических факторов.
В основе подкласса моделей на основе макроэкономических показателей лежит идея о том, что вероятность дефолта государственных, корпоративных и розничных заемщиков банка имеет циклический характер и возрастает во время экономической рецессии. Как правило, в таких моделях используется регрессионный анализ, в котором участвуют какие-либо макроэкономические показатели: ВВП, инфляция, курс национальной валюты, уровень безработицы и др. С их помощью можно получить не только краткосрочную, но и долгосрочную оценку вероятности дефолта заемщика. Такой метод оценки долгосрочной вероятности дефолта носит название Through The Cycle estimation (TTC). [3, C.40–42].
Обычно заемщиков делят по секторам экономики или индустрии, в которой они действуют. В качестве факторов модели выбираются ставка роста ВВП, уровень потребительских цен, уровень инфляции, уровень безработицы и т. д. Значение каждого фактора, в свою очередь, определяется по его предыдущим показателям согласно авторегрессионной модели AR порядка q [1, C.60]:
Xit = bio + bi1Xit-1 + … + biqXit-q + vit.
Эти данные используются для моделирования совместного распределения величин вероятностей дефолта и переходных вероятностей для тех или иных секторов экономики или индустрии. Риски каждого сегмента далее агрегируют (с учетом значений корреляций и спрогнозированного значения состояния данного сегмента). Затем при помощи метода Монте Карло модель генерирует совместное распределение убытков в результате дефолта для всех сегментов портфеля. Несмотря на то что данная модель не позволяет определить вероятность дефолта детально по каждому контрагенту, т. к. анализ строится на уровне сегментов экономики, она незаменима для оценки по портфелю спекулятивных инструментов, которые наиболее чувствительны к экономическим циклам и первыми реагируют на изменения в экономике.
Сильной стороной моделей на основе макроэкономических факторов является то, что с их помощью можно учесть циклический характер вероятности дефолта и получить долгосрочную оценку. Часто они используются для стресс-тестирования других моделей вероятности дефолта. Кроме того, ввиду доступности статистики по макроэкономическим показателям данный подход можно использовать для кросс-анализа вероятности дефолта заемщиков, имеющих различную географическую принадлежность (например, для банков разных стран). Однако слабой стороной является тот факт, что для удачного применения данных моделей необходимо использовать показатели, относящиеся к одному бизнес-циклу, а определить периодичность циклов в экономике достаточно затруднительно. Более того макроэкономические показатели могут служить лишь расширением модели, т. к. на их основе сложно оценить вероятность дефолта конкретного заемщика. Выходом из этой ситуации может быть совмещение двух моделей. Сначала с помощью модели на основе финансовых показателей прогнозируется дефолт для каждой компании, далее корректируется на макроэкономические изменения, которые как раз и будут подсчитаны с помощью макромоделей. Этот вывод еще раз подчеркивает актуальность поставленной задачи.
В качестве факторов для оценки были выбраны основные макроэкономические показатели: ВВП, курс рубля, инфляция и т.д. Однако эмпирическим путем обосновывается взаимосвязь только с тремя из них: ВВП в постоянных ценах, цена на нефть и динамика реальных располагаемых расходов населения (с остальными на практике связь подтвердить не удалось).
Экономическим обоснованием выбора трех факторов служит их влияние на экономику в целом. ВВП является главным индикатором национальной экономики, другими словами, агрегированным показателем результативности каждой компании и государства в целом. Таким образом, его изменение может отражать ту или иную ситуацию в национальном хозяйстве. Однако для анализа и сравнения реальных изменений лучше использовать ВВП в постоянных ценах, из которого исключено влияние изменения уровня цен в стране. Цена на нефть выбрана в связи со спецификой экономики России, в которой долгие годы преобладает экспортно-сырьевая модель. От цен на углеводороды зависит значительная часть доходов бюджета, стабильность курса рубля и экономическая политика государства. Динамика реальных располагаемых доходов населения показывает покупательную способность населения, от которой зависят доходы компаний.
Проанализировав экономические аспекты зависимости переменных, автор пришел к выводу, что в данной работе будет рассматриваться модель линейной множественной регрессии, которая в общем виде записывается как:
yt = a0 + a1х1t + a2х2t +a3х3t +ut,
где yt – зависимая величина, х1t, х2t, х3t – объясняющая (независимая) переменная, а а0, а1, a2, a3 – параметры уравнения, ut – случайный остаток.
В нашем случае в качестве переменной yt будет выступать доля дефолтных компаний в общей структуре юридических лиц, а х1t – ВВП в постоянных ценах, х2t – динамика реальных располагаемых доходов населения, х3t – цена на нефть. Индекс t отражает учет временного фактора, в нашем случае текущие эндогенные факторы объясняются текущими экзогенными.
Если говорить о виде зависимостей в модели, то динамика реальных располагаемых доходов и цена на нефть очевидно имеет обратную связь с долей дефолтных компаний. С показателем объема внутреннего валового продукта нельзя сказать однозначно: с одной стороны, его увеличение показывает экономический рост, что должно улучшить финансовые показатели компаний, с другой стороны, экономический рост провоцирует большую конкуренцию на рынке, таким образом, увеличивая дефолтные компании (санирующая функция рынка).
На основе вышесказанного, можно записать финальный вид спецификации:
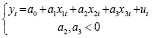
Данная форма спецификации представляет собой приведенную форму, так как эндогенная переменная выражена через экзогенные.
Далее происходил сбор статистических данных из Росстата, Центра макроэкономического анализа и краткосрочного прогнозирования, ФНС и других источников. Доля банкротов рассчитывалась, как отношение количества банкротов в том или ином периоде на общее количество юридических лиц. Каждый период соответствует одному кварталу, так как годовые значения не показывают полной картины динамики показателей, а некоторые переменные не имеют точных месячных показателей. Было взято 50 значений для обучающей и 4 для контрольной (поквартальные значения с 2003 по 2017). [2, 4, 5, 6].
Следующим шагом является нахождение оптимальных оценок параметров, для этого воспользуемся методом наименьших квадратов. Для использования МНК, в основе которого лежит использование теоремы Гаусса-Маркова, необходимо проверить выполнение трех её предпосылок.
Первая предпосылка теоремы Гаусса-Маркова гласит, что математическое ожидание случайных возмущений во всех наблюдениях равно нулю: E(ut) = 0 [1, C.153]. Для выполнения этой предпосылки необходимо, чтобы уравнение регрессии в спецификации модели было составлено правильно. Проверим на качественность спецификацию при помощи F-теста. В F-тесте мы сравниваем значения F, полученного при расчете функции ЛИНЕЙН, и F итического, полученного путем расчета в Excel через функцию =F.ОБР.ПХ(α=0,05;v1=k; v2=n–(k+1))= 3,15990759. Так, F = 21,41509469, что больше Fкр, равного 4,043. Из этого следует, что спецификация является качественной.
Вторая предпосылка теоремы гласит, что дисперсия случайных возмущений во всех случаях наблюдений равна константе, то есть: Var (ut) = σu. Для проверки данной предпосылки проведем тест Голдфелда-Квандта [1, C.186–189]. Упорядочим уравнения наблюдений и по одинаковому количеству первых и последних уравнений оценим МНК модель, определив суммы квадратов остатков ESS1 = 0,00937846 и ESS2 = 0,01022747. Статистика Голдфелда-Квандта: GQ = ESS1/ESS2= 0,916987313, 1/GQ = ESS2/ESS1= 1,090527629. Fкр=F.ОБР.ПХ(α;ν_1;ν_2)=3,78704354. Так как Fкр> 1/GQ и Fкр>GQ, то вторая предпосылка теоремы выполняется. Значит, проявляется гомоскедастичность случайных остатков.
Третья предпосылка теоремы гласит, что ковариация между парами случайных возмущений в наблюдениях равны нулю, то есть случайные возмущения в наблюдениях независимы: Сov (ui; uj) = 0 (i≠j). [1, C.193–196].
Для подтверждения данной предпосылки проведем тест Дарбина-Уотсона. Рассчитаем статистику Дарбина-Уотсона: DW = 1,908742936. По параметрам n=50 и k=3 определяем критические границы интервала для статистики (dL; dU) по таблице: dL= 0,832; dU= 1,407. Построим интервалы (рисунок).

Интервальные значения для теста Дарбина-Уотсона
Значения статистики DW попадает в интервал М3, что говорит об отсутствие связи, автокорреляции случайных остатков, то есть Сov (ui ;uj) = 0 (i≠j). Третья предпосылка теоремы выполняется.
Четвертая предпосылка теоремы заключается в том, что ковариация между вектором регрессоров и вектором случайных переменных равна нулю, то есть регрессоры и случайные возмущения независимы: Cov (ui; xki) = 0. Так как xki – константа, то это априори справедливо. То есть четвертая предпосылка теоремы Гаусса-Маркова выполняется. [1, C.153]
Таким образом, все предпосылки теоремы Гаусса-Маркова выполняются.
Теперь методом наименьших квадратов в Excel при помощи функции ЛИНЕЙН получаем набор оценок параметров:
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 = 0,781142467 |
|
То есть оцененный вид модели записывается следующим образом:

Как видим, стандартные ошибки коэффициентов, как и дисперсия, находятся на достаточно низком уровне. Также в данном случае R–критерий равен 0,781142467, что говорит о высоком уровне связи между эндогенной и экзогенными переменными. Значение коэффициента показывает, что уравнением регрессии объясняется приблизительно 78 % дисперсии результативного признака, а на долю прочих факторов приходится 22 % её дисперсии. Однако необходимо также рассчитать R2 скорректированный, чтобы исключить искусственное завышение показателя из-за количества факторов. R2 скорректированный = 0,744666211, что также подтверждает высокую зависимость показателей.
Проверим адекватность модели при помощи метода интервального прогнозирования. Метод интервального прогнозирования заключается в сравнении показателя yt из контрольного набора с интервалом, граничными значениями, которого являются 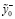 и
и 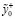 . Данные значения определяются по следующим формулам:
. Данные значения определяются по следующим формулам:
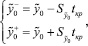
где 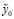 – оцененное значение эндогенной переменной; tкр. – критическое значение функции, распределённой по закону Стьюдента, рассчитываемое в Excel по формуле СТЬЮДЕНТ.ОБР.2Х=2,010634758;
– оцененное значение эндогенной переменной; tкр. – критическое значение функции, распределённой по закону Стьюдента, рассчитываемое в Excel по формуле СТЬЮДЕНТ.ОБР.2Х=2,010634758; 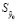 – средняя квадратическая ошибка прогноза, рассчитываемая по формуле
– средняя квадратическая ошибка прогноза, рассчитываемая по формуле 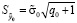 . Теперь рассчитаем границы интервалов и сравним с показателями из контрольной выборки: 0,331334966∈(-0,306845202; 0,969515134); 0,370134149∈(-0,237607525; 0,977875822); 0,411299502∈(-0,229601117; 1,052200121); 0,460040173∈(-0,152402131; 1,072482477).
. Теперь рассчитаем границы интервалов и сравним с показателями из контрольной выборки: 0,331334966∈(-0,306845202; 0,969515134); 0,370134149∈(-0,237607525; 0,977875822); 0,411299502∈(-0,229601117; 1,052200121); 0,460040173∈(-0,152402131; 1,072482477).
На основании полученных данных можно прийти к выводу, что модель адекватна.
Составленная модель зависимости доли дефолтных компаний в общей структуре юридических лиц от трех макроэкономических факторов является адекватной, а ее спецификация – качественной. Коэффициент детерминации показывает на высокий уровень связи между переменными. Модель была разработана, оценена и проверена по критериям качественности и адекватности, так же проверены предпосылки теоремы Гаусса-Маркова.
Практическое применение модели в будущем имеет большой потенциал. Она позволит учитывать основные изменения в экономике, вводить различные макроэкономические сценарии, учитывать цикличность экономики, а также проводить стресс-тестирования и кросс-анализ. Комплексное использование вместе с моделями, построенными на финансовых результатах позволит избежать проблему сложности при оценке дефолта конкретного заемщика. Таким образом, кредитные организации смогут более точно оценивать кредитоспособность своих клиентов и снизить риск кредитного портфеля в целом.
Библиографическая ссылка
Мякишева Д.А. АНАЛИЗ ЗАВИСИМОСТИ ДОЛИ ДЕФОЛТНЫХ КОМПАНИЙ В ОБЩЕЙ СТРУКТУРЕ ЮРИДИЧЕСКИХ ЛИЦ ОТ МАКРОЭКОНОМИЧЕСКИХ ФАКТОРОВ // Международный студенческий научный вестник. – 2018. – № 4-6. ;URL: https://eduherald.ru/ru/article/view?id=19034 (дата обращения: 27.07.2024).