Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гайворон А.Н. 1 Писарева А.М. 1

---

1 ФГБОУ ВО «Ставропольский государственный аграрный университет»

Человек, который выдвигает для рынка новое лекарство, которое может спасти человеческие жизни, считается капиталистом. Ученые бывают очень довольны, когда есть кто-нибудь, кто может применить итоги их работ в жизни. Однако многие коммунисты полагают, что ученым и артистам необходимо трудиться для общества и получать за собственную работу не более чем кто-либо другой. Общепринятой сейчас является точка зрения на математическую статистику как на науку об общих способах обработки результатов эксперимента. Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирования эксперимента), в ходе исследования (последовательный анализ). Её можно определить как науку о принятии решений в условии неопределённости. Кратко, можно сказать, задача математической статистики состоит в создании методов сбора и обработки статистических данных.

Статья в формате PDF

0 KB

Лекарство

наблюдения

ученые

эффективность

выздоровление

вероятность

статистка

фармацевтическая промышленность

1. Бондаренко В.А., Мамаев И.И. Профессиональная направленность в обучении математике студентов биологических факультетов // Вестник АПК Ставрополья. – 2014. – № 1 (13). – С. 6–9.

2. Бондаренко Д.В., Бражнев С.М., Литвин Д.Б., Варнавский А.А. Метод повышения точности измерения векторных величин // Наука Парк. – 2013. – № 6 (16). – С. 66–69.

3. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика: рабочая тетрадь. – Ставрополь, 2015.

4. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Совершенствование экономических механизмов для решения проблем экологической безопасности. // Информационные системы и технологии как фактор развития экономики региона: II Международная научно-практическая конференция. – 2013. – С. 68–71.

5. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Финансовая математика в инвестиционном проектировании (учебное пособие) // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 8–2. – С. 178–179.

6. Литвин Д.Б., Шепеть И.П. Моделирование роста производства с учетом инвестиций и выбытием фондов. // Социально-экономические и информационные проблемы устойчивого развития региона: Международная научно-практическая конференция. -2015. – С. 114–116.

7. Литвин Д.Б., Шепеть И.П., Бондарев В.Г., Литвина Е.Д. Применение дифференциального исчисления функций нескольких переменных к разработке алгоритма определения координат объекта // Финансово-экономические и учетно-аналитические проблемы развития региона: Материалы Ежегодной 78-й научно-практической конференции. – 2014. – С. 242–246.

8. Роговая Н.А., Шайтор А.К., Литвин Д.Б. Качество образования и один из путей его повышения. // Инновационные направления развития в образовании, экономике, технике и технологиях. Международная научно-практическая конференция: сборник статей в 2–частях. под общей редакцией В.Е. Жидкова. – 2014. – С. 169–173.

9. Litvin D., Ghazwan R.Q. Thinking skills product in mathematics among the students of the university // Экономические, инновационные и информационные проблемы развития региона: материалы Международной научно-практической конференции. – 2014. – С. 5–9.

10. Litvin D.B. Mathematical self-concept among university students // Аграрная наука, творчество, рост: Сборник научных трудов по материалам IV Международной научно-практической конференции. – 2014. – С. 326–329.

Если новое лекарство получает распространение, то связано ли это с ускорением выздоровлений. Аналогично, новое лекарство может оказаться эффективным в каждом из десяти различных госпиталей, но объединение результатов укажет на то, что это лекарство либо бесполезно, либо вредно. Подтвердить выдвинутую тему хотелось бы следующим примером.

В результате длительных наблюдений установлено, что вероятность полного выздоровления больного, принимавшего лекарства А, равна 0,8. Новое лекарство В было назначено 800 больным, причём 660 из них полностью выздоровели, то есть относительная частота выздоровлений w=660/800=0,825 стала выше. Можно ли считать новое лекарство значимо эффективнее лекарства А на пятипроцентном уровне значимости?

По условию задачи примем в качестве нулевой гипотезы 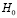гипотезу о том, что вероятность выздоровления 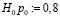. Поскольку по результатам наблюдения w = 660/800 = 0,825, что больше чем по нулевой гипотезе 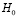, то в качестве альтернативной гипотезы примем следующую: 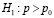, что соответствует правосторонней критической области [5, 9].

Нам необходимо выяснить, является ли новое лекарство эффективнее старого. В качестве критерия возьмём величину

,

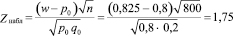где 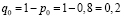, значение которой подчиняется стандартному нормальному распределению.

Критическое значение критерия Zкр определим в зависимости от альтернативной гипотезы (типа критической области) с использованием функции Лапласа по формуле [3, 7]

,

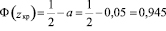откуда по таблице функции Лапласа 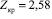. Поскольку 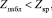1,75 < 2,58, то нет оснований отвергнуть нулевую гипотезу H0, то есть w=0,825 обусловлена случайностью выборки.

Найдём интервальную оценку для вероятности выздоровления.

Если n > 30 и np >10, то распределение случайной величины

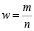
можно аппроксимировать нормальным распределением 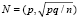. Следовательно, при этих же условиях распределение величины

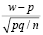
близко к нормальному с нулевым математическим ожиданием и единичной дисперсией [1, 8].

По аналогии, найдем такое число t, для которого справедливо равенство

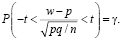
Это число t является корнем уравнения F(t) = g/2, где F(t) – функция Лапласа.

Неравенство, стоящее в скобках, разрешим относительно р. Для этого неравенство перепишем в виде эквивалентного неравенства

.

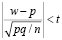Возведем в квадрат, в результате получим

.

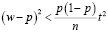Далее, возведя в квадрат (w – p) и перенеся все члены влево, получим

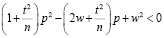[2,6].

Корни p1 и p2 этого квадратного трехчлена являются границами интервальной оценки вероятности события и определяются выражениями

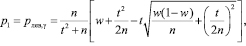
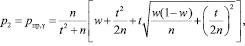
где n – общее число испытаний; w – относительная частота; t – значение аргумента функции Лапласа, при

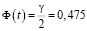
(g(0,95) – заданная надежность), t=1,96.

Если n >> 100, то в формулах слагаемым 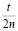можно пренебречь, тогда для вычисления 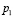и 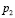, можно использовать приближенные формулы [4,6]:

, .

,

.

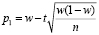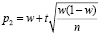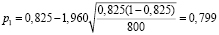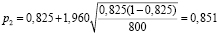Из этого следует вывод, что лекарство В не эффективнее чем А, поскольку доверительный интервал для p c надежностью γ=0.95 равен:

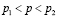, 0,799 < p < 0,851.

На сегодняшний день можно полагать конкретным, что одной из главных причин, которые подводят к привычному применению лекарств, злоупотреблению ими и, в итоге, развитию токсикомании, служит способность приводить в повышенное настроение, эйфорию. Помимо этого, до сегодняшнего дня создаются все новые лекарства, которые приводят к ощущению прилива сил, бодрости, хорошего настроения, а опасность их игнорируется либо преуменьшается. Сегодня ведется спор о том, прослеживается ли настоящая токсикомания при использовании амфетаминов (фенамина, первитина), однако с каждым годом растет количество описанных в литературе моментов злоупотребления данными средствами и вызываемых ими психозов.

Фармацевтическая промышленность считается наиболее прибыльной среди всех отраслей хозяйства. Если производство медикаментов подчинено в первую очередь коммерческим интересам, если оно выступает частным бизнесом, то о важной осторожности при открытии нового лекарства, зачастую не думают.

Политики и утомленная довольством общественность в небольшом количестве богатых странах могут позволить себе роскошь поговорить о пище Франкенштейна – там кризис перепроизводства еды, однако даже в Европе никто не изъявляет желания умирать от воспаления легких либо же страдать от недостатка ключевых витаминов, по данной причине никто не нападает на новые лекарства и витамины [10].

Новый режим, который предполагает сингулярность конечного времени может заново запустить гонку за рост, даже в более ускоренном режиме, который возрастет благодаря новым открытиям, которые дадут возможность человечеству в полном объеме задействовать большие ресурсы океанов либо даже ресурсы других планет, в основном, которые располагаются вне нашей солнечной системы. Для достижения планет необходимы новые методы более ускоренного передвижения, а также революции в нашем контроле над плохими биологическими результатами космоса на людей с его нулевой гравитацией и высокой радиацией. Новые лекарства и генная инженерия могут дать возможность людям быть готовыми к трудностям космоса, подталкивая к новой эре улучшенного быстрого роста после времени консолидации, которая находится на самой высокой точке в новой сингулярности конечного времени, через столетия в будущем.

Библиографическая ссылка