Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Агаджанян И.Д. 1 Коростылёва А.Е. 1 Лопатина Д.В. 1

---

1 ФГБОУ ВО «Ставропольский государственный аграрный университет»

Выполнен анализ современных методов экспериментального исследования динамики распространения примесей в атмосфере и изменений ее показателей. Для математической модели оценки концентрации аэрозольных примесей, полученной на основе фундаментальной системы решений однородного дифференциального уравнения второго порядка с постоянными коэффициентами выполнено построение вычислительного алгоритма, его программная реализация, а также проведены численные исследования вычислительного алгоритма на сходимость и устойчивость получаемых решений к погрешностям в исходных данных. В связи с ростом антропогенной нагрузки на экологические системы, в том числе и на атмосферу, увеличивается актуальность развития методов и средств исследования ее состояния для решения экологических проблем.

Статья в формате PDF

0 KB

загрязнение атмосферы

математическое моделирование

уравнение переноса

дифференциальное уравнение

аналитическое решение

вычислительный алгоритм

численные исследования

1. Наац В.И. Качественная модель оценки концентрации аэрозольных примесей в атмосфере, основанная на интегральном представлении решения уравнения турбулентной диффузии / В.И. Наац, Е.П. Ярцева // Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. – 2012. – № 1. – С. 38 – 43.

2. Наац В.И. Математические модели и вычислительный эксперимент в проблеме контроля и прогноза экологического состояния атмосферы / В.И. Наац, И.Э. Наац, Р.А. Рыскаленко, Е.П. Ярцева. – Ставрополь: Изд-во СКФУ, 2016. – 376 с.

3. Наац В.И. Обратные задачи и качественные модели в проблеме мониторинга атмосферы / В.И. Наац, Р.А. Рыскаленко, Е.П. Ярцева. – LAP LAMBERT Academic Publishing. – 2015. – 405 с.

4. Наац В.И. Построение рекурсивно-итерационного алгоритма для трехмерного нестационарного уравнения переноса примесей в атмосфере / В.И. Наац, Е.П. Ярцева // Вестник Северо – Кавказского федерального университета. – 2014. – № 2 (41). – С. 9 – 14.

5. Наац В.И. Разработка качественной модели и итерационного алгоритма для оценки концентрации загрязняющих примесей в атмосфере / В.И. Наац, Е.П. Ярцева // Вестник Северо – Кавказского федерального университета. – 2013. – № 1 (34). – С. 15 – 21.

6. Наац В.И. Численное исследование рекурсивных и итерационных алгоритмов в задаче моделирования переноса аэрозолей в атмосфере / В.И. Наац, Е.П. Ярцева // Вестник Ставропольского государственного университета. – 2011. – Выпуск 75 [4]. – С. 44 – 50.

7. Наац И.Э. Операторы потенциального типа в задачах прикладного анализа / И.Э. Наац, В.И. Наац, Р.А. Рыскаленко, Е.П. Ярцева // Наука. Инновации. Технологии: Научный журнал Северо-Кавказского федерального университета. – Ставрополь, 2017. – № 3. – С. 43 – 60.

8. Ярцева Е.П. Программа для реализации рекурсивных и итерационных вычислительных алгоритмов для пространственной задачи переноса загрязняющих примесей в турбулентной атмосфере. Свидетельство о государственной регистрации программы для ЭВМ № 2014661580. Зарегистрировано в Реестре программ для ЭВМ 31 октября 2014.

9. Ярцева Е.П. Качественная модель оценки концентрации аэрозольных примесей в атмосфере на основе итерационного метода / Е.П. Ярцева // Наука и устойчивое развитие: материалы VII Всероссийской научно-практической конференции молодых ученых. – Нальчик. – 2013. – С. 176 – 178.

10. Ярцева, Е.П. Построение модульной системы «Математические модели и вычислительные алгоритмы оценки концентрации загрязняющих примесей в турбулентной атмосфере» / Е.П. Ярцева // Наука и образование XXI века: сборник статей Международной научно – практической конференции. – Уфа. – 2014. – Часть 2. – С. 5 – 7.

В связи с ростом антропогенной нагрузки на экологические системы, в том числе и на атмосферу, увеличивается актуальность развития методов и средств исследования ее состояния для решения экологических проблем. В рамках обозначенной задачи необходимы анализ процессов и прогнозирование последствий распространения загрязняющих веществ в атмосфере [1, 2].

Исследование динамики распространения примесей в атмосфере и изменений ее показателей экспериментально, значительно затруднено в силу сложного характера диффузионного и конвективного массопереноса. Помимо этого определенную сложность вызывает как наблюдение за ходом эксперимента, так и интерпретация полученных данных с целью выявления структуры движения вследствие значительных масштабов объектов исследования и длительности процессов конвекции и диффузии. Известно, что существующие современные методы экспериментального исследования требуют использования дорогостоящего измерительного оборудования и экспериментальных установок. В тех случаях, когда масштабы возможных техногенных нарушений исключают натурные испытания, а лабораторные исследования в силу ограниченных возможностей обеспечения подобия дают лишь неполную информацию, математическое моделирование и вычислительный эксперимент становятся основными способами изучения процессов переноса вещества в турбулентной атмосфере [1, 2].

Современная вычислительная техника позволяет создавать эффективные вычислительные алгоритмы и комплексы программ для решения указанной задачи [9, 10, 13]. Однако численное моделирование на ЭВМ предъявляет к исследователю серьезные требования, помимо отличной подготовки по вычислительной математике и программированию, он должен хорошо разбираться в физических особенностях решаемой задачи, а также верно интерпретировать результаты моделирования.

В решении данных задач особое внимание уделяется моделированию с помощью дифференциальных уравнений, так как рассматриваемые процессы протекают как во времени, так и в пространстве. Дифференциальные уравнения описывают динамику процесса переноса примесей в режиме реального времени, однако следует отметить ряд возникающих на пути имитаций с помощью дифференциальных уравнений, трудностей. Во – первых, систематических правил получения самих уравнений не существует, их составление основано на полуэмпирических закономерностях, аналогиях, рассуждениях и навыках моделирующего, о чем уже упомянуто выше. Во – вторых, решаемые задачи имеют большую размерность, что определяет технические трудности. В связи с этим можно утверждать, что реализация описываемых моделей на параллельных компьютерных системах является актуальной научной задачей.

Математическая модель переноса загрязняющих примесей в атмосфере использует уравнения математической физики для установления взаимосвязей между неизвестными функциями, характеризующими исследуемый объект. Уравнения дополняются неравенствами и другими ограничениями, связанными с моделью. Математические вопросы корректности моделей (существование и единственность решения, его устойчивость) являются очень важными, но не всегда решаемыми.

Перенос загрязняющей субстанции q в пограничном слое атмосферы описывается нестационарным уравнением переноса (с учетом его параметризации) [3, 6, 14]:

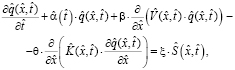(1)

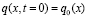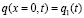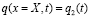, , , (2)

где 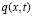– поле концентрации примесей (загрязняющей субстанции), 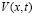– скорость ветра, 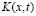– атмосферная турбулентность, 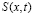– источник примесей.

В данной работе помимо известных двух итерационных схем решения уравнения переноса субстанции в турбулентной среде [4, 5] рассматриваются другие формы интегральных уравнений и соответствующие им преобразования интегральной модели [11, 12]. Настоящий метод носит исключительно качественный характер, его основное назначение состоит в разработке методик качественной оценки значений параметров в задачах математического моделирования явления переноса загрязняющей примеси в турбулентной атмосфере.

Уравнение (1) запишем следующим образом:

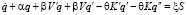, (3)

где

;

;

;

;

;

;

;

;

.

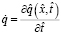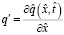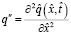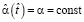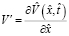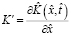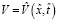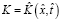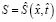В результате последующих преобразований уравнения (3) приходим к параметризованной модели:

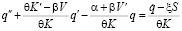, (4)

где далее примем следующие обозначения:

,

,

,

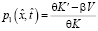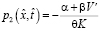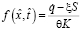в соответствии с чем уравнение (4) получим в виде:

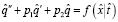. (5)

Уравнение (5), как известно [2, 7], представляет собой дифференциальное уравнение второго порядка с постоянными коэффициентами и имеет аналитическое решение.

Далее в работе выполняется построение вычислительного алгоритма решения уравнения переноса (5) с использованием рекурсивной вычислительной схемы:

,

,

,

,

,

,

,

,

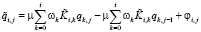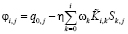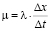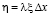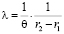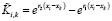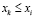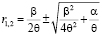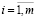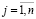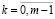; ; . (6)

Алгоритм вычислительной модели (6) достаточно прост, в то же время, погрешность получаемых с его помощью решений зависит от погрешностей аппроксимации искомого решения и полей исходных данных, а также их производных [8, 15]. В силу указанных обстоятельств далее проводятся численные исследования рекурсивного алгоритма (6) на сходимость и устойчивость получаемых решений. Для проведения вычислительного эксперимента, кроме алгоритма, разработано программное обеспечение (в системе Maple) и тестовые задачи [11, 12, 14]. Установлено, что увеличение размерности расчетной сетки приводит к росту погрешности, что хорошо объясняется ростом вычислительных погрешностей, которые несут в себе исходные данные. Так, в случае размерности 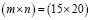погрешность решения составила 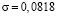. Анализ результатов вычислительного эксперимента показывает, что, если погрешность в данных экологического мониторинга до 8 %, то вычислительный алгоритм (6) сохраняет свойство устойчивости при соответствующем выборе исходных данных.

Библиографическая ссылка