Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Карасева Е.А. 1 Мартышкин А.И. 1

---

1 Пензенский государственный технологический университет

В статье предлагаются некоторые модели, по которым можно проводить анализ критериев производительности механизмов доступа к общим ресурсам многопроцессорных систем. Для достижения указанной выше цели в статье используются положения и методы теории массового обслуживания. Подробно описываются модели для управления общими ресурсами многопроцессорных систем. Основными полученными в работе результатами являются выражения для времени ожидания задач в вычислительной системе, верифицированные путем моделирования. Анализ результатов показал, что планирование на основе приоритетов дает выигрыш по времени ожидания в очереди к семафору почти в 2 раза, чем при использовании стратегии на основе FIFO. Полученные модели позволяют произвести количественные оценки времени ожидания процессов, обращающихся к общему ресурсу через посредство семафора. Модели могут быть использованы при проектировании параллельных ОС, где критичным является время выполнения процессов.

Статья в формате PDF

0 KB

многопроцессорная система

моделирование

теория массового обслуживания

общий ресурс

семафор

пользовательское пространство

пространство ядра операционной системы

1. Алиев Т.И. Основы моделирования дискретных систем. – СПб.: СПбГУ ИТМО, 2009. – 363 с.

2. Карасева Е.А., Мартышкин А.И. Обзор средств управления процессами и ресурсами многопроцессорных операционных систем // Международный студенческий научный вестник. – 2016. – № 3–1. – С. 80–81.

3. Мартышкин А.И., Карасева Е.А. Исследование сетевых математических моделей управления одиночными критическими ресурсами в многопроцессорных системах // XXI век: итоги прошлого и проблемы настоящего плюс. – 2016. – № 3 (31). – С. 179–184.

4. Мартышкин А.И., Карасева Е.А. К вопросу моделирования и исследования процесса управления множеством критических ресурсов в многопроцессорных системах // Инновации в науке. – 2016. – № 55–2. – С. 76–83.

5. Мартышкин А.И., Карасева Е.А. Математические модели для качественной оценки производительности семафоров многопроцессорных вычислительных систем // Инновации в науке. – 2015. – №50. – С. 40–45.

6. Мартышкин А.И., Карасева Е.А. Математическое моделирование процесса управления одиночными критическими ресурсами в многопроцессорных системах // Современные методы и средства обработки пространственно-временных сигналов: сборник статей XIV Всероссийской научно-технической конференции / Под ред. И.И. Сальникова. 2016. – С. 110–114.

7. Таненбаум Э., Бос Х. Современные операционные системы. – СПб.: Питер, 2015. – 1120 с.

Существуют два метода синхронизации взаимодействующих процессов: метод взаимных исключений и барьерная синхронизация, способам и средствам реализации которой посвящена работа [7]. В этой статье отчасти показаны методы реализации взаимных исключений, к которым относят блокирующие переменные, мьютексы, семафоры, мониторы. Наиболее общим из них является семафор, т.к. битовый семафор заменяет собой и блокирующую переменную, и мьютекс. Более того, семафоры используются для входа в монитор и обеспечения взаимоисключения внутри монитора. Поэтому в дальнейшем будем все средства синхронизации называть семафором [2, 5]. Семафоры используются для координации использования одиночных или фиксированного множества общих ресурсов (ОР) несколькими процессами. Проблема заключается в том, что взаимодействующие процессы такого рода приводят к столкновению транзакций, поскольку они вступают в конфликт друг с другом, что в свою очередь приводит к потерям производительности операционной системы (ОС) в целом. Наиболее явно это проявляется в параллельных системах, когда взаимодействующие процессы реализуются в независимых процессорах (ЦП), которые могут потребовать одновременно ОР.

Если ОР требуется слишком большому числу ЦП, то они ставятся в очередь к семафору. По мере освобождения ОР запросы удовлетворяются традиционно по принципу: первым пришел – первым обслужен (FIFO). Там, где разрешена параллельная обработка и имеется единица ОР, некоторый процесс может держать его продолжительное время. В это время другие процессы будут ожидать окончания этого процесса, причем быстро исполняющиеся процессы скоро «застрянут» в более медленных [7].

Аналитическая модель n-процессорной системы с одиночным ОР для оценки потерь производительности из-за конфликтов за доступ к семафору, при использовании концепции планирования типа FIFO, изображена на рис. 1а [3, 6]. Математическая модель представлена в виде разомкнутой стохастической сети массового обслуживания (РСеМО), состоящей из n (S1,…,Sn) одноканальных систем массового обслуживания (СМО), моделирующих ЦП, и одноканальной СМО (Sn+1), которая моделирует семафор. Причем СМО S0 выступает в качестве внешнего источника запросов (заявок на выполнение процессов), которые могут формироваться, например, терминалами пользователей, а также в качестве поглотителя обслуженных заявок [4].

Пусть на вход n-процессорной системы поступает поток запросов на выполнение процессов с интенсивностью λ0 = 1/T, где T – средняя длительность интервала между поступающими на вход запросами. Поток запросов распределяется предварительным планировщиком по ЦП с вероятностями р01,…,роn (см. граф вероятностей передач стохастической сети, изображенной на рис. б). Каждый ЦП содержит собственный планировщик, формирующий очередь запросов Оi. Будем считать, что время выполнения запроса vi в каждом ЦП распределено по экспоненциальному закону.

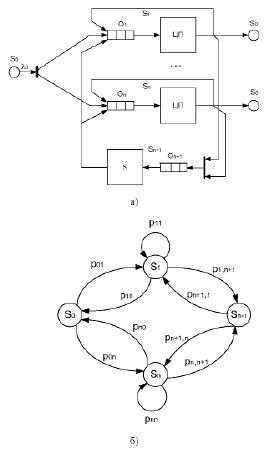
Схема аналитической модели n-процессорной системы (а) и её граф передач (б)

Предположим для упрощения, что потоки запросов на выполнение процессов на входе многопроцессорной системы распределяются равновероятно по ЦП, т.е. р01=…= роn = 1/n (см. рис. б). Причем i-й ЦП (СМО S1,…,Sn), обслужив очередную заявку, передает её на обслуживание в семафор (СМО Sn+1) с вероятностями p1, n+1 =,…,= pn,n+1 (т.е. каждый ЦП формирует потоки запросов семафора с одинаковой интенсивностью). Заявки, получившие обслуживание в семафоре, с равной вероятностью возвращаются на продолжение обслуживания в ЦП, следовательно, pn+1,1 =…= pn+1,n = 1/n. Предположим также, что вероятность получения заявкой полного обслуживания в i-м ЦП (вероятность выхода заявки из сети) составляет pi0, а вероятность, что заявка останется на обслуживании в СМО Si, составляет pij, где i,j = 1,…,n.

Пусть среднее время обслуживания i-го процесса в семафоре сравнимо со временем обслуживания его в ЦП, и конкретные значения ti могут отличаться в среднем не более чем в 2–3 раза. Для конкретности примем, что среднее время обслуживания в ЦП составляет vi = 1 единицу (i = 1,…,n) времени, а среднее значение в семафоре

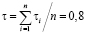
единиц времени.

Будем считать, что в среднем на одну реализацию некоторого процесса приходится 1000 циклов обращения к семафору. Тогда вероятность того, что заявка покинет вычислительную систему (процесс полностью выполнился) составит pi0 = 0,001. Вероятность же того, что заявка останется на обслуживании в вычислительной системе составит (1 – pi0) = 0,999.

Время ожидания заявки в сети

Tw = α1tw1 + α2tw2 + ... + αntwn + αn+1 twn+1,

где αi = λi / λ0 – коэффициент передачи сети (i = 1, ..., n + 1); twi – время ожидания в i-й СМО [1]. Интенсивности потоков заявок определятся системой уравнений:

,

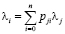где pji – вероятность передачи из СМО Sj в СМО Si; i, j = 0, 1, ..., n + 1.

В статье показано, что планирование на основе приоритетов дает выигрыш по времени ожидания в очереди к семафору почти в 2 раза, чем при использовании стратегии на основе FIFO. Полученные модели позволяют произвести количественные оценки времени ожидания процессов, обращающихся к общему ресурсу через посредство семафора. Модели могут быть использованы при проектировании параллельных ОС, где критичным является время выполнения процессов.

Работа выполнена при финансовой поддержке РФФИ (Проект № 16–07–00012 А).

Библиографическая ссылка