Сейчас наблюдается развитие различных подходов, связанных с проведением оценки характеристик рассеяния электромагнитных волн на сложных объектах. Если говорить о практическом применении, то интересует формирование комбинированных методов, которые дают возможность уменьшения времени, требуемого для осуществления расчетов с сохранением необходимой точности расчетов [5, 8].
При построении решений совокупности прикладных проблем электродинамики и теории антенных структур часто необходимо проводить анализ электромагнитных полей, рассеянных проводящими объектами, которые располагаются на небольших расстоятиях друг по отношению к другу.
Среди подобных задач можно выделить задачи, связанные с расчетом ближнего поля в апертурных антеннах, полей апертур для областей, находящихся вне телесных углов по основному излучению, когда есть необходимость того, чтобы учитывать влияние подстилающих поверхностей и других материальных объектов, которые находятся на небольшом расстоянии относительно антенны, например, это могут быть затеняющие конструкции из металла, импедансные структуры и др.
Целью данной работы является рассмотрение методики расчета характеристик рассеяния электромагнитных волн в рамках итеративного алгоритма для периодических структур.
В каскадной модели, исследователь осуществляет переход от одного шага к другому строгим последовательным образом.
В отличие от каскадного способа, при итеративном способе разработку разбивают по нескольким итерациям, и в процессе каждой из них идет выполнение практически всех видов работ, и, как результат идет формирование реально работающей системы при постоянным образом совершенствующихся функциональных возможностей.
Большей частью для всех итераций идет выполнение и проведение анализа требований, и процессы проектирования, и тестирования.
Например, в самой первой итерации, еще до того выявились все требования, может произойти разработка прототипов, на которых идет проверка основных архитектурных решений. По мере того, как детализируются требования по отдельным компонентам в ходе дальнейших итераций, идет их формирование.
Можно указать достоинства такого подхода. В процессе разработок всегда возникают дополнительные требования со стороны исследователя или идет изменение сформулированных им до этого требований.
Кроме этого возникают новые ограничения, которые связаны с существующими подходами. Наиболее полным образом их можно учесть как раз в итерационных разработках, так как при таких подходах решение задач в большой мере готово к тому, что будут изменения.
Итерационные процессы заключаются в том, что идет последовательное уточнение начального приближения. Каждый из таких шагов называют итерацией.
Для такого этапа при вычислении каждого из решений при точности применяют некоторый итерационный подход, который дает возможности для построения последовательности приближений к решению.
В том случае, когда последовательность приближений сходится к решению, тогда итерационный метод называют сходящимся.
Для итерационного метода утверждают, что он является одношаговым, если при вычислении очередного приближения необходимо применять одно предыдущее приближение.
Многошаговый итерационный метод будет в том случае, когда при вычислении очередного приближения необходимо использовать несколько предыдущих приближений.
Среди важных характеристик в итерационных методах можно отметить скорость сходимости.
За счет применения совокупности известных подходов по формальному представления сторонних источников подобные проблемы можно свести к интегральным уравнениям второго рода, которые имеют смысл граничных условий для магнитного вектора относительно криволинейных поверхностей в идеальном проводнике, в них искомой функцией будет поверхностный ток или магнитное поле, которое является эквивалентным для него.
Интегральные уравнения второго рода в своих областях использования имеют ряд определенных достоинств, одним из них является устойчивость решений по отношению к малым возмущениям во входных параметрах задач.
При расчетах мы использовали уравнение Фредгольма первого рода, описывающего плотность искомого электрического тока, которое относится к случаю Е-поляризации [4].
Осуществлялось решение уравнения на основе метода моментов [4], проводилась его дискретизация. В результате образуется система линейных алгебраических уравнений. После решения этой системы определяются продольные электрические токи.
Во многих случаях, чем более точным образом базисными функциями идет передача характера действительных распределений токов на излучателях, тем будут лучше характеристики сходимости и для некоторых случаев более будет обусловлена матрица импедансов (при этом будет более устойчивым решение).
Проводится расчет двумерной эффективной площади рассеяния (ЭПР) исследуемого объекта. Объект представлял собой решетку из семи двумерных равносторонних треугольников, имеющих длину стороны r, которые находятся друг относительно друга на расстоянии заданного шага S (рис. 1).
Когда мы проводили оценку характеристик рассеяния на основе метода интегральных уравнений, был применен алгоритм расчета для всей решетки, то есть контур проходил по всем треугольникам.
В качестве центрального момента при проведении записей интегральных операторов можно отметить решение задач о том, как возбуждается анализируемая структура при помощи произвольной комбинации электрических и магнитных токов.
Основная идея метода интегральных уравнений состоит в следующем:
1. Процессы исследования полей в неоднородных средах сводят к тому, что идут их расчеты в однородной среде.
2. Учет влияния на поля неоднородностей (в случае, когда есть диэлектрические, проводящие и магнитные тела) происходит за счет введения в поля вторичных источников – заряды поляризаций, токи намагниченности наведенных вихревых токов и т.д., которые распределены на границах (по объему) неоднородностей.
3. Вначале идет определение интегральных уравнений, для которых должно быть соответствие распределению вторичных источников, потом на основе уравнений поля при учете исходных и вторичных источников идет решение задачи анализа полей.
4. Интегральные уравнения решают при помощи компьютеров.
В качестве естественных граничных условий в идеальном проводнике можно указать равенство нулю полей в его внутренней области.
При решении интегрального уравнения может быть использован метод моментов.
Метод моментов представляет собой аналитический приближенный способ решения краевой задачи, при нем решение ищется как линейная комбинация по линейно независимым функциям , она дает удовлетворение граничным условиям.
Если говорить о качестве такого метода вследствие того, что вычисляется среднеквадратичное отклонение по отрезку решения в рамках метода моментов и точного решения, то можно увидеть, что:
• качество в приближенном решении растет, когда увеличивается количество точек разбиения;
• в случаях, когда быстро осциллирующие решения погрешность решения определяется не только числом точек разбиения, но и способом их выбора. Меньшую погрешность получаем, если точки разбиения будут попадать на места, которые будут соответствовать пучностям в колебательном процессе;
• есть или нет однородностей по граничным условиям – это практически не оказывает влияния на то, какое качество решений;
• для точек разбиения есть различия в приближенных и точных решениях.
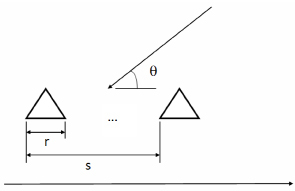
Рис. 1. Рассеяние электромагнитной волны, которая E-поляризована на решетке, сформированной из семи цилиндров с треугольным поперечным сечением
В качестве базисных функций может быть рассмотрен вейвлет-базис. Для таких случаев приходят к псевдоразреженной матрице импедансов, это дает возможности для экономии машинного времени когда решается система, и еще память компьютера во время заполнения такой матрицы, за счет использования разреженных технологий.
Но этой ситуации заполнение матрицы в системе линейных уравнений происходит весьма долгим образом, поскольку трудно предсказывать расположение малых значений в матрице и, поэтому, сложно сформировать эффективным образом функционирующий алгоритм.
В данной работе для решения интегрального уравнения использовался итерационный подход, позволяющий уменьшить время решения по сравнению с методом интегральных уравнений.
При формировании итерационной процедуры в качестве основы был применен подход, связанный с разбиением объекта на кластеры [9].
В данной статье мы рассматривали взаимодействие между ближайшими частями объекта [1, 2, 6].
При проведении исследований мы делали сравнение средней ЭПР, которая была вычислена на основе использования двух подходов (метод интегральных уравнений применялся нами для имитации эксперимента).
Сектор углов наблюдения составлял 30о. Мы считали, что разница для средних ЭПР, получаемых на основе применения этих двух методов не должна быть более 3 дБ [3]. Расчеты показали, что необходимо, чтобы минимальным значением было M=5.
Разработанная методика позволила получить результаты расчетов ЭПР исследуемой решетки, которая формировалась из равносторонних треугольников со стороной 0.05<r/l< 1 и шага решетки 0.15<S/l<3, где l – длина электромагнитной волны.
Путем варьирования значений шага решетки и стороны была осуществлена оценка границ, в которых находится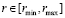 
при определенном значении шага решетки S, который дает максимальную эффективность работы итерационного подхода. На рис. 2 приведена зависимость rmax(S).
Можно убедиться в том, что идет увеличение диапазона значений r при увеличении значений S.
Проведенный анализ позволил установить, что итерационный метод ведет к тому, что времени уменьшается более чем в два раза по сравнению с использованием метода моментов.
Можно на рис. 2 увидеть зависимость rmax(S), которая получилась при осуществлении расчета на базе итерационного подхода для ЭПР анализируемого объекта. Были достигнуты значения разницы в ЭПР, рассчитанной на основе метода интегральных уравнений, а также итерационного подхода, которые не превышали 3 дБ (этим подразумевалась экспериментальная погрешность).
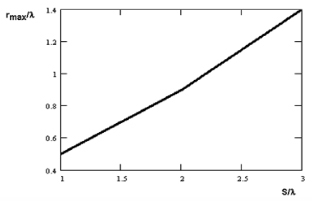
Рис. 2. Зависимость rmax(S), при которой работоспособен итерационный подход, когда оценивается средняя ЭПР объекта
Таким образом, в работе проведен анализ возможностей использования итерационного подхода для оценки характеристик рассеяния объектов сложной формы на примере периодических структур. Были получены результаты, показывающие снижение времени, необходимого для оценки рассеивающих характеристик, в несколько раз.
Библиографическая ссылка
Агулов И.С. ПРОВЕДЕНИЕ МОДЕЛИРОВАНИЯ РАССЕЯНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН НА ПЕРИОДИЧЕСКОЙ СТРУКТУРЕ НА ОСНОВЕ ИТЕРАТИВНОГО ПОДХОДА // Международный студенческий научный вестник. – 2017. – № 4-9. ;URL: https://eduherald.ru/ru/article/view?id=17714 (дата обращения: 21.11.2024).