В радиофизических исследованиях и радиолокационных их направлениях, которые имеют практические приложения, при наблюдающемся бурном и повсеместном распространении и применении информационных технологий мы можем определить научные, методические и технологические компоненты, с использованием которых происходит модернизация действующих и формирование принципиально новейших систем, лежащих в сферах радиосвязи, навигации, дистанционных зондирований и локационных направлениях [4, 6].
В них проводят изучение вопросов, связанных с тем, как происходит распространение радиоволн в пространстве и каким образом идут процессы их рассеяния на объектах, имеющих сложную электрофизическую структуру и пространственную конфигурацию, которые относятся к естественным, и они создаются людьми [5].
Поскольку указанные проблемы являются комплексными и многогранными, то при их рассмотрении, исторически образом сложилось так, что ученые ограничивались изучением фундаментальных закономерностей, которые касались рассмотрения канонических задач, связанных с дифракцией для объектов, имеющих простую форму, или они разрабатывали эвристические методы, имеющие некоторые упрощения, которые не давали возможностей для того, чтобы получать необходимую точность для результатов [7].
Мы имеем возможности убедиться, что происходит накопление заметного научно-практического потенциала в сфере, связанной с вычислительными методами и средствами, который позволяет эффективным способом осуществлять разнообразное практическое применение фундаментальных электродинамических и радиофизических разработок [5].
Однако при применении формальных попыток, касающихся непосредственного использования фундаментальных электродинамических методик, когда рассматриваются вопросы, связанные с рассеянием радиоволн для реальных объектов, со сложной электрофизической структуры и пространственными конфигурациями с включением свойств подстилающих поверхностей, не только будут иметь ограничения, но и практически неразрешимы, в условиях использования суперкомпьютеров.
Исходя из вышесказанного, задачи исследований, которые требуется решать с целью того, чтобы разрабатывать эффективные, универсальные и современные способы расчетов электромагнитных полей, рассеиваемых объектами, должны быть ориентированы на то, чтобы проводить анализ и широкомасштабное использование современных численных методик и способов, должны обеспечивать ускорение вычислений.
На рисунке приведена схема рассеяния электромагнитных волн на исследуемом объекте.
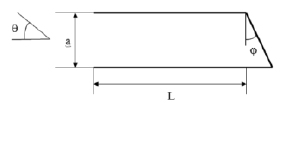
Схема рассеяния электромагнитных волн на полой структуре с размером апертуры a и длиной L, θ – угол наблюдения
Оценка характеристик рассеяния электромагнитных волн в случае E-поляризации проводилась на основе метода интегральных уравнений [6].
Решалась задача определения угла раскрыва апертуры полой структуры [2] a, при котором достигается максимальное значение средней эффективной площади рассеяния в секторе углов [9] наблюдения 25 ° ≤ q ≤ 33 °. Размеры структуры были следующие: a = 3.6l, L = 7.1l, где l – длина падающей электромагнитной волны [1, 3]. Для этого использовался метод оптимизации, базирующийся на муравьином алгоритме.
В муравьином алгоритме использовалось следующее правило перехода [10]:
Муравей, находящийся в точке r, будет выбирать следующую точку s исходя из следующих уравнений:
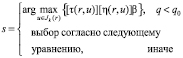, (1)
где jk(r) – множество ячеек сетки которые необходимо посетить муравью k, расположенному в точке сетки r, τ(r, s) – мера феромона,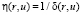 
, где вес δ(r, u) выбирался как расстояние между точками, q – случайная величина, q0 – параметр (
).
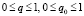Если q ≥ q0, муравей будет выбирать следующую точку согласно следующему уравнению:
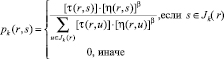, (2)
где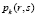 
– вероятность точки s быть выбранной муравьем k, расположенным в точке r.
Правило локального обновления:
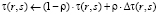, (3)
где ρ – локальный параметр, 0 > > > 1, Δτ(r, s) – величина суммы феромона, оставленного муравьями. Глобальное правило обновления соответствует следующему уравнению:
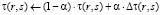, (4)
где α – глобальный параметр, 0 > α > 1, Δτ(r, s) = 1/лучшая глобальная длина, если отрезок (r, s) принадлежит этой длине.
В результате математического моделирования было установлено, что максимальное значение средней эффективной площади рассеяния в указанном секторе углов наблюдения достигается для угла наблюдения a = 23 °.
Библиографическая ссылка
Чупракова И.С. О РЕШЕНИИ ПРОБЛЕМ, СВЯЗАННЫХ С РАСЧЕТОМ ХАРАКТЕРИСТИК РАССЕЯНИЯ ОБЪЕКТОВ // Международный студенческий научный вестник. – 2017. – № 4-7. ;URL: https://eduherald.ru/ru/article/view?id=17629 (дата обращения: 23.11.2024).