Методы дискретной математики (методы формализованного представления) часто используются для анализа, исследования управленческих задач и их решения, а также для моделирования объектов исследования и применяются в таких отраслях экономики, как математическое моделирование, логистика, эконометрика. В число этих методов входят методы, которые базируются на теоретико-множественных представлениях, математической логике, графах и других разделах математики [1]. В эконометрике, например, используются булевские переменные для построения регрессионных моделей по неоднородным данным и для анализа регрессионных моделей с переменной структурой. В данном случае исследуется только одно уравнение регрессии, в которое добавляются булевские переменные, характеризующие изучаемый фактор. Этим методом очень удобно пользоваться, если есть необходимость установить зависимость модели от какого-либо фактора.
Если в логистике требуется задать маршруты или описать потоки, то удобнее всего будет применить теорию графов. Здесь схему дорог мы можем изобразить, как ориентированный граф, и далее выбрать самый короткий маршрут. Что же касается теории нечетких множеств, то с ее помощью можно правильно сделать выбор в пользу конкурентоспособного товара или услуги методом нечеткого предпочтения, поэтому эта теория используется в маркетологии, когда нужно проанализировать рынки экономических благ [3].
Рассмотрим практическое применение «жадного» алгоритма, который заключается в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным. В этом алгоритме пересеклись интересы дискретной математики и исследования операций [4]. Например, в городе Невинномысске находятся предприятия и они поставляют свою продукцию в магазины, кафе и аптеки этого города. Специалисты определили возможные дорожные маршруты для того, чтобы проложить все коммуникации, и выяснили, сколько денежных средств потребуется для создания коммуникаций для каждой трассы. Итак, проложить коммуникаций для дороги между фабрикой одежды и магазином обуви составляет 15 ден. ед., между фабрикой одежды и мебельным заводом – 85 ден. ед., между фабрикой одежды и кондитерской фабрикой составляет 20 ден. ед., между магазином обуви и мебельным заводом – 25 ден. ед., между магазином обуви и обувным заводом – 65 ден. ед. Стоимость прокладки коммуникаций для трассы, которая соединяет кондитерскую фабрику и магазин продуктов – 5 ден. ед., между кондитерской фабрикой и рестораном – 50 ден. ед., между мебельным заводом и рестораном – 20 ден. ед., между магазином продуктов и хозяйственным магазином составляет 20 ден. ед., между хозяйственным магазином и обувным заводом – 25 ден. ед., между хозяйственным магазином и рестораном – 35 ден. ед., между обувным заводом и овощным магазином – 15 ден. ед., между обувным заводом и аптекой составляет 40 ден. ед., между рестораном и аптекой – 10 ден. ед., между овощным магазином и торговым центром – 20 ден. ед., между аптекой и металлургическим заводом составляет 30 ден. ед., между аптекой и торговым центром – 45 ден. ед., между металлургическим заводом и торговым центром, – 25 ден. ед. Необходимо найти такую структуру сети, при которой коммуникации связали бы все пункты, а затраты на прокладку этих коммуникаций были бы минимальны.
Введём обозначения: V1 – фабрика одежды, V2 – магазин обуви, V3 – кондитерская фабрика, V4 – мебельный завод, V5 – магазин продуктов, V6 – хозяйственный магазин, V7 – обувной завод, V8 – ресторан, V9 – овощной магазин, V10 – аптека, V11 – металлургический завод, V12 – торговый центр. При создании графической интерпретации данной модели нам становится понятно, что получился граф, который содержит 12 вершин и 18 ребер. Для решения задачи необходимо дерево покрытия минимального веса. Эта задача решается алгоритмом «краскала» – разновидностью «жадного» алгоритма.
Пусть имеется конечное непустое множество E,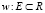 
– функция, которая ставит в соответствие каждому элементу e этого множества неотрицательное действительное число, w(e) – вес элемента e и семейство 
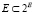. Вес w(X) найдем сложением весов всех элементов множества X. Нам нужно из данного семейства выбрать непустое подмножество с наименьшим весом.
Всем пунктам сети поставим в соответствие вершины графа G, а всем ребрам графа поставим в соответствие число, которое равно сумме денежных средств, необходимых для строительства соответствующей коммуникации, связывающей объекты.
Из всех ребер выбирается ребро с наименьшим весом (исходя из алгоритма Краскала). В нашем случае таким ребром является ребро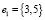 
, получаем граф T1. Далее строится граф T2, равный сумме 
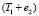, где – ребро, которое имеет самый маленький вес среди тех ребер, которые не входят в граф T1, и не составляющий циклов с ребрами T2, 
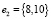. Граф T3 находится сложением T2 и e3, где e3 = {7, 9}. Аналогично находим графы T4-T11.
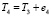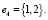
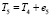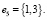
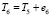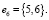
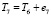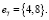
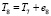, где 
, где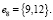 
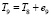, где 
, где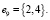 
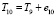, где 
, где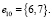 
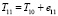, где 
, где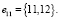 
Таким образом, мы нашли минимальное дерево покрытия взвешенного графа, а значит, определили оптимальную структуру сети, в которой денежные средства, которые необходимо потратить на прокладку коммуникаций, рассчитываются следующим образом:
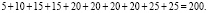
Из всех возможных затрат эта сумма является наименьшей.
Итак, при прокладке коммуникационной сети, которая должна соединить все указанные объекты, затрачивается 200 ден. ед. Коммуникации будут проложены между следующими объектами: аптека – ресторан – мебельный завод – магазин обуви – фабрика одежды – кондитерская фабрика – магазин продуктов – хозяйственный магазин – обувной завод – овощной магазин – торговый центр – металлургический завод.
Разберем задачу «коммивояжера» как ещё один пример применения средств дискретной математики в экономике [2]. Представителю страховой фирмы необходимо выехать из Ставрополя, объехать 6 населенных пунктов и вернуться назад. Между пунктами проложены дороги. Расстояние между Ставрополем и Михайловском составляет 6 км, между Ставрополем и Пелагиадой – 7 км, между Ставрополем и Надеждой расстояние составляет 20 км, между Ставрополем и Татаркой – 12 км, между Ставрополем и Рождественским – 10 км. Между Михайловском и Пелагиадой расстояние составляет 5 км, между Михайловском и Надеждой – 7 км, между Михайловском и Татаркой – 9 км, между Михайловском и Рождественским – 16 км. Между Пелагиадой и Надеждой расстояние составляет 4 км, между Пелагиадой и Татаркой – 10 км, между Пелагиадой и Рождественским – 12 км. Между Надеждой и Татаркой расстояние – 3 км, между Надеждой и Рождественским – 15 км. Между Татаркой и Надеждой – 6 км, между Татаркой и Рождественским – 4 км, между Рождественским и Пелагиадой – 11 км, между Рождественским и Татаркой – 21 км. Представитель страховой фирмы должен объехать все порученные ему пункты по одному разу и вернуться назад за самый короткий срок или с наименьшими затратами на проезд.
Для решения данной задачи построим матрицу A, отображающую расстояние между городами i и j, при этом i ≠ j. Если i = j, то ставим символ ∞, так как такой дороги не существует. В нашем случае матрица примет вид:
Матрица A строится для того, чтобы в каждой строке и в каждом столбце получить не менее одного кратчайшего маршрута (нулевого приведенного значения). Для этого в каждой строке матрицы A от каждого элемента мы вычитаем значение минимального элемента этой строки [6]. В результате получим:
Вычисляем теперь коэффициент приведения. Он равен сумме всех минимальных элементов матрицы A, которые были вычтены из строк и столбцов:
kпр = 6 + 5 + 4 + 3 + 4 + 10 = 20.
Вычисляем коэффициенты значимости для каждого занулившегося элемента.
k23 = 2, k34 = 1 + 2 = 3, k45 = 5, k61 = 2, k56 = 2 + 4 = 6.
Теперь из матрицы нужно вычеркнуть строку и столбец, в которых находится элемент с наибольшим коэффициентом значимости. В нашем случае таким элементом является а56: коэффициент значимости равен 6. Для элемента а56 установим значение 1: а56 = 1.
После преобразований получим:
Опять вычисляем коэффициенты значимости:
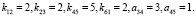
Матрица уменьшается в размере:
Для новой матрицы находим коэффициенты значимости:
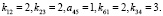
Теперь матрица запишется в виде:
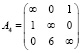
Коэффициенты значимости последней матрицы:
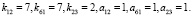
Выбираем элементы матрицы с наибольшими коэффициентами значимости: а56, а45, а34, а12, а61, а23, их индексы указывают нам те рёбра, которые должны войти в маршрут.
Таким образом, в маршрут представителя страховой фирмы вошли ребра: {5,6}, {4,5}, {3,4}, {1,2}, {6,1}, {2,3}. Все вершины (пункты) соединились.
Длина маршрута составляет:
.
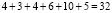Путь торговца включает расстояния между городами {Ставрополь, Михайловск}, {Михайловск, Пелагиада}, {Пелагиада, Надежда}, {Надежда, Татарка}, {Татарка, Рождественский}, {Рождественский, Ставрополь} и имеет длину, равную 32 километрам.
В данной статье были рассмотрены такие разделы дискретной математики как применение алгоритма «краскала», решена задача «коммивояжера» венгерским методом, методом совершенного «паросочетания». Применение методов дискретной математики доказывает на примерах, что играет важную роль в экономической сфере, а также способствует эффективной деятельности экономики в целом [5].
Библиографическая ссылка
Кармова Д.А., Мисходжев А.Б. ИСПОЛЬЗОВАНИЕ МЕТОДОВ ДИСКРЕТНОЙ МАТЕМАТИКИ В ЭКОНОМЧЕСКИХ ИССЛЕДОВАНИЯХ // Международный студенческий научный вестник. – 2017. – № 4-4. ;URL: https://eduherald.ru/ru/article/view?id=17428 (дата обращения: 23.11.2024).