Увеличение прибыли и минимизация издержек – основные проблемы для любой фирмы. Правильное и рациональное управление запасами поможет выбрать правильный размер одной партии товара для поставки таким образом, чтобы уменьшить годовые затраты и тем самым решить одну из проблем производства. В связи с этим, каждому экономисту важно знать, как правильно определить размер одной партии.
В этом случаи не обойтись без математики. Три основные модели помогу правильно определить ситуацию и при правильных математических вычислениях достичь желаемого результата.
Чтобы не ошибиться в выборе ситуации существует три модели: «Основная модель» (партия поступает на склад мгновенно, когда запас становится равным нулю), «Модель производственных поставок» (запас пополняется, когда возникает дефицит, при помощи производственной линии) и «Модель поставок со скидкой» (если размер партии достаточно велик, то товар может поставляться по льготной цене).
Обозначим основные величины:
1. Цена единицы товара – c (у.е.);
2. Интенсивность спроса товара в год – d (ед.);
3. Организационные издержки за одну партию товара – s (у.е.);
4. Издержки на хранение единицы запаса товара в год – h (у.е.);
5. Размер одной партии товара – q (ед.).
Рассмотрим на конкретном примере, какие математические действия требуются для расчёта партии товара.
Интенсивность равномерного спроса составляет 2 тыс.ед. товара в год. Товар поставляется с конвейера, производительность которого составляет 6 тыс. ед. в год. Организационные издержки равны 15 у.е., издержки на хранение – 2 у.е., цена ед. товара – 3 у.е. Чему равен оптимальный размер партии?
Из условия нам известна производительность конвейера, что говорит нам о модели производственных поставок. Эта модель требует следующих вычислений:
По условию: d = 2000, c = 3, h = 2, s = 15, p = 6000.
Найдём оптимальный размер партии:
С = cd + 
+ 
.
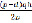C(q) = 3*2000 +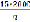 
+
.
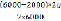q* = 
= 
=
= 
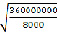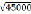=212 – оптимальный размер партии
Оптимальное число поставок за 1 год
n* = d / q* = 2000 / 212 = 9.
Продолжительность поставки
τ* = q* / p = (212 / 6000) ×365 = 13 дней.
Продолжительность цикла изменения запаса
t* = 365 / n* = 365 / 9 = 41 дней.
Прибегнув к несложным математическим вычислениям, мы смогли определить оптимальное количество размера партии и числа поставок.
Тем самым экономист, умеющий управлять запасами, сможет выбрать правильный вариант поставки и минимизировать годовые затраты фирмы.
Библиографическая ссылка
Королева А.В., Сабинина А.С., Зотова С.А., Светличная В.Б., Матвеева Т.А. МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14158 (дата обращения: 19.04.2024).