Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Файлы
• Литература

Донец З.Г. 1 Иванова Ю.А. 1 Иванова А.А. 1

---

1 Ставропольский государственный аграрный университет

Статья в формате PDF

336 KB

1. Прохоренкова А.Т. Курс лекций по дисциплине «Теория вероятностей и математическая статистика». Часть 1 // Теория вероятностей. – Смоленск: СИБП, 2012. – 100 с.

2. Мелешко С.В., Невидомская И.А., Донец З.Г. Организация самостоятельной работы студентов при изучении комбинаторики // Учетно-аналитические и финансово-экономические проблемы развития региона. – 2012. – С. 289-292.

3. Невидомская И.А., Якубова А.М. Применение факторного анализа при исследовании экономических процессов // Современные наукоемкие технологии. – 2013. – № 6. – С. 81-83.

4. Донец З.Г., Мамаев И.И., Шибаев В.П. Учебная дисциплина как целостная модель организации обучения студентов на интегративной основе // Теоретические и прикладные проблемы современной педагогики. – 2012. – С. 40-47.

5. Теория вероятностей и математическая статистика / А.Ф. Долгополова, Т.А. Гулай, Д.Б. Литвин, С.В. Мелешко // Международный журнал экспериментального образования. – 2012. – № 11. – С. 51-52.

Возможное значение случайной величины определяется одним числом, то она называется одномерной. Например, число очков, выпадающее при бросании кости (дискретная одномерная случайная величина, расстояние от орудия до места падения снаряда (непрерывная одномерная случайная величина).

Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, ..., n числами., их называются соответственно двумерными, трехмерными, ... , n-мерными.

Двумерную случайную величину обозначают (X, Y), их называют составляющей; величины X и Y , образуют систему двух случайных величин. Аналогично n-мерную величину можно рассматривать как систему п случайных величин.

Для дискретной случайной величины ξ, принимающей значения х=х1,х2… с вероятностями Рξ(х), т.ч. , .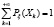

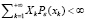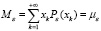
Математическое ожидание 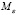используют как характеристику положения распределения ξ.

Для непрерывной случайной величины ξ с плотностью вероятности 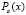, т.ч.

математическим ожиданием называется

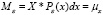
Ковариацией случайных величин ξ и η называется величина

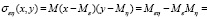
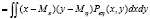
Связь между величинами является функциональная зависимость. В этом случае каждому значению одной величины соответствует вполне определенное одно или несколько значений другой величины. Однако существуют такие связи между величинами, которые нельзя отнести к типу функциональных зависимостей.

Ковариация .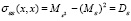

Абсолютное значение ковариации 2х случайных величин не превосходит произведения стандартных отклонений этих случайных величин, т.е.

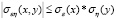
Следовательно, называемая коэффициентом корреляции нормированная величина находится в диапазоне от [-1;1]. Теснота зависимости двух случайных величин определяется коэффициентом корреляции.

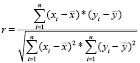
Свойства коэффициента корреляции:

1. При 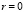связь между величинами отсутствует.

2. При связь между величинами становится функциональной.

3. При 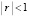связь между величинами устанавливается по шкале Чеддока:

В уравнении 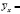ах + b величина x является факторным признаком, а величина 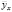– результативным признаком.

Число 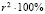показывает, сколько процентов общей вариации объясняется изменением факторного признака.

Ковариация и коэффициент корреляции являются мерами линейной статистической связи различных случайных величин. Понятие линейной статистической связи отличается от понятия линейной связи или линейной зависимости так же как случайная величина отличается от детерминированной величины.

Коэффициент корреляции обладает следующими свойствами:

- Он не меняется, если к значениям ξ и η

- При умножении случайных величин на положительные числа, то это также не влияет на величину коэффициента корреляции

- При умножение случайных величин на -1 умножается и коэффициент корреляции

- 2 случайные величины, коэффициент корреляции равен 0, называются некоррелированными. Если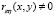 , то он своей величиной характеризует не только наличие, но и ему линейной и статистической связи: чем больнее его абсолютная величина, тем сильнее эта связь (корреляция). Максимальная корреляция равна значениям 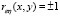. Если 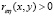, ξ и η с точностью до случайных погрешностей одновременно возрастают \ убывают. Если же 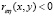, то с возрастанием одной случайной величины, другая убывает.

Библиографическая ссылка