Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Файлы
• Литература

Гайчук В.Д. 1

---

1 Ставропольский государственный аграрный университет

Статья в формате PDF

318 KB

1. Агроинженерия (электронный учебно-методический комплекс) / Попова С.В., Смирнова Н.Б., Долгих Е.В., Крон Р.В. // Международный журнал экспериментального образования. – 2009. – № S4.

2. Комплект рабочих тетрадей по курсу высшей математики для инженерных специальностей / Попова С.В., Крон Р.В., Смирнова Н.Б., Долгих Е.В., Морозова О.В., Долгополова А.Ф., Тынянко Н.Н. // Международный журнал экспериментального образования. – 2009. – № S4. – С. 14-15.

3. Попова С.В., Смирнова Н.Б. О прикладной направленности математики в высшей школе // Информационные системы и технологии как фактор развития экономики региона: сб. научных статей по материалам Международной науч.-практ. конф. – Ставрополь: АГРУС Ставропольского ГАУ, 2013. – С. 260-264.

4. Линейная алгебра: учебное пособие / Крон Р.В., Попова С.В., Долгих Е.В., Смирнова Н.Б. // Международный журнал экспериментального образования. – 2014. – № 11-1. – С. 115.

5. Математика: учебное пособие / Крон Р.В., Попова С.В., Долгих Е.В., Смирнова Н.Б. // Международный журнал экспериментального образования. – 2014. – № 11-1. – С. 114-115.

6. Немцова А.В., Попова С.В. Применение средств матричной алгебры для решения задач экономического содержания // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 171-172.

7. Бондаренко В.А., Мамаев И.И. Экономико-математическое моделирование: сущность и этапы // Учетно-аналитические и финансово-экономические проблемы развития региона: сб. трудов ежегодной 76-й научно-практической конференции Ставропольского государственного аграрного университета «Аграрная наука - Северо-Кавказскому региону». – Ставрополь, 2012. – С. 277-280.

8. Вахтина Е.А., Габриелян Ш.Ж. Электротехника и электроника. – Москва, Изд-во «Илекса», 2012.

Одной из возможных областей применения средств линейной алгебрыявляетсяраздел электротехники, занимающийся расчетами контурных токов в цепи. Для решения задачэлектротехники используется матричное уравнение контурных токов, системы линейных уравнений, определители. Рассмотрим применение этого аппарата более подробно.

В методе контурных токов принято считать, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляются относительно контурных токов. После нахождения решений уравнений определяют токи ветвей через контурные токи.

Следовательно, метод контурных токов можно определить как метод расчета, в котором за неизвестные принимаются контурные токи.

Контурные токи – это условные, расчетные токи. Обозначим их двойными индексами: I₁₁, I₂₂, I₃₃. Число переменных в этом методе равно числу независимых контуров, то есть числу уравнений, составляемых по второму закону Кирхгофа.

В этом случае задача расчета токов разделяется на две части:

1) рассчитываются контурные токи I₁₁, I₂₂, I₃₃.

2)рассчитываются реальные токи.

Для лучшего понимания зададим условие конкретной схемой (см. рис. 1)/

Для данной схемы известны следующие значения: Е₁ = 8В, Е₂ = 12В, Е₃ = 19В, R₁ = 9Oм, R₂ = 20Oм, R₃ = 12Oм, R₄ = 19Oм, R₅ = 14Oм, R₆ = 10Oм.

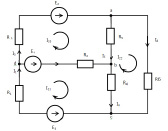
Рис. 1. Схема электрической цепи

В процессе решения задачи электротехники привлекаются математические способы записи условий и алгоритмы, позволяющие найти математическое решение поставленной задачи, в частности, системы линейных алгебраических уравнений, матрицы, определители.

Матрицы применяются для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов – количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Переведём поставленную задачу расчёта контурных токов на язык математики,учитывая порядок расчета токов:

а) выберем независимые контуры , , ;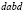

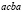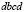б) выберем направления контурных токов (по часовой стрелке);

в) выберем направления обхода контуров (по часовой стрелке);

г) составим для каждого контура уравнение по второму закону Кирхгофа,учитывая, что через сопротивления, входящие в два соседних контура проходят два контурных тока.

Рассмотрим схему электрической цепи, представленной на рисунке 1. Направления обхода контуров показаны стрелками и обозначены I₁₁, I₂₂, I₃₃. По второму закону Кирхгофа уравнения для этих контуров примут следующий вид (1):

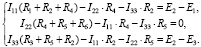
Арифметическая сумма сопротивлений, входящих в каждый выбранный контур, будетсобственным контурным сопротивлением Rkk (с двойным индексом номера контура) и определяется по формулам:

R₁₁ = R₁ + R₂ + R₄,

R₂₂ = R₄ + R₅ + R₆,

R₃₃ = R₃ + R₅ + R₂.

Сопротивления, входящие в два соседних контура, будутобщими сопротивлениями контура. Например, сопротивление R₄ является общим между первым и вторым контурами, обозначим его также двойным индексом – по номерам контуров.

Например, R₄ = R₁₂ = R₂₁.

Алгебраическая сумма ЭДС, входящих в данный контур, будетконтурной ЭДС, её также обозначим двойными индексами:

Е₁₁ = Е₂ – Е₁ – контурная ЭДС первого контура;

Е₂₂ = 0 – контурная ЭДС второго контура;

Е₃₃ = Е₂ – Е₃ – контурная ЭДС третьего контура.

Учитывая все выше перечисленные факты и обозначения,запишем систему уравнений (1) в другом виде.Для решения получаем новую компактную систему с определенным размещением слагаемых с токами I₁₁, I₂₂, I₃₃ в виде соотношения 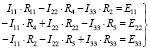(2):

(2)

Введём обозначения:

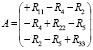– матрица коэффициентов при переменных I₁₁, I₂₂, I₃₃,

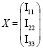– матрица-столбец переменных I₁₁, I₂₂, I₃₃,

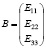– матрица-столбец свободных членов,

то составленная система примет классический вид матричного уравнения .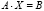

В дальнейшем будем решать полученную систему с помощью определителей.

Общее решение системы из трех уравнений относительно тока Ikk имеет вид:

,

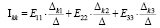где Δ – главный определитель системы уравнений (2);

Δ_kp – алгебраические дополнения, получаемые из определителя Δ посредством вычеркивания k-й строки и p-го столбца и умножения полученного определителя на знак .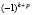

Далее вычислимглавный определитель системы (2) и дополнения к нему:

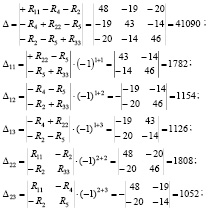
И т.д.

В определитель системы уравнений со знаком (+) войдут только собственные сопротивления R₁₁, R₂₂, R₃₃, остальные члены все отрицательные.

Если провести из левого верхнего угла определителя диагональ в нижний правый угол и учесть что R12 = R21 и вообще R_km = Rm_k, то можно убедиться, что определитель главной диагональю делится на две половины, являющиеся зеркальным изображением одна другой, то есть является симметричным. Тогда в силу симметрии будут равны и дополнения с индексами

Δ_km = Δ_mk (3)

Используя выражение (3), получим:

Δ₁₂ = Δ₂₁ = 1154; Δ₁₃ = Δ₃₁ = 1126; Δ₃₂ = Δ₂₃ = 1052. (4)

Используя значения (4), запишем выражения для контурных токов:

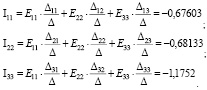
Проанализировав схему на рисунке 1, определяем реальные токи во всех ветвях схемы:

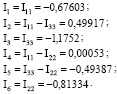
Проведенные исследования позволяют сделать вывод о том, что математический аппарат теории матриц имеет широкий спектр применения. В частности, позволяет решать задачи анализа электрических цепей методом контурных токов. Использование матричного аппарата позволяет значительно упростить проводимые расчеты.

Библиографическая ссылка