Постановка задачи: построить интегральную модель системы образования, учитывающую процессы обучения и самообучения работников и учеников (например, студентов) системы образования, а также непосредственное воздействие внешней среды на эту систему, и найти колебательные решения некоторых уравнений этой модели.
Актуальность поставленной задачи. Повышение эффективности и качества получения среднего и высшего образования всегда были и остаются актуальными вопросами теории и практики педагогики. Практика успешного применения математической теории развивающихся систем при моделировании экономических, технических, биологических и др. систем подсказывает возможность применения полученных результатов и для моделирования задач управления качеством получаемого образования, в частности обучения и самообучения студентов.
Анализ исследований и публикаций. Впервые уравнения академика В.М. Глушкова, моделирующие динамику развивающейся системы (РС) [2,4,7-9], применялись для описания функционирования учебного заведения или любой системы образования в [8, с.234,235]. В предложенной там модели часть ранее созданных в единицу времени рабочих мест работников учебного заведения по новейшей технологии (в качестве показателя эффективности которой принимается ее производительность или удельная относительная скорость) воссоздает в единицу времени новые рабочие места работников учебного заведения, другие их части используются: 1) для создания самой вышеуказанной технологии, 2) для создания других новейших технологий, применяемых для осуществления выпуска в единицу времени закончивших полный образовательный курс (дипломированных специалистов), 3) для осуществления главной (внешней) функции учебного заведения – выпуска в единицу времени дипломированных специалистов. Эта модель с заданной начальной предысторией предусматривает сворачивание устаревших технологий, применяемых работниками учебного заведения, однако в ней никак не учитывается непосредственное воздействие на деятельность учебного заведения внешних (для рассматриваемого процесса) факторов и не рассматриваются важнейшие вопросы получения образования, связанные с качеством (или эффективностью) подготовки дипломированных специалистов и сворачиванием устаревших технологий, применяемых учениками учебного заведения при самостоятельном усвоении переданных им знаний. В [1] была предпринята попытка построить математическую теорию обучения в системе образования с учетом вышеизложенных вопросов качества подготовки дипломированных специалистов (для чего понадобилось вводить понятие нового рабочего места не только для работников, но и для учеников учебного заведения) и влияния внешней среды. Заметим, что в [4, с. 112-122] и [9, с. 262-266] были выявлены колебательные и волновые процессы динамики РС, колебательные режимы в случае нелинейного вида модельных функций, найдены солитонные решения уравнений модели РС. Однако в исследуемых уравнениях не учитывалось непосредственное воздействие внешней среды на РС. Поэтому естественно возникают постановки более общих задач (в частности, поставленной выше).
Цель статьи состоит в решении поставленной выше задачи.
Изложение основного материала. Под рабочим местом (РМ) работника системы образования (СО) или студента будем понимать совокупность трудовых (учебных) функций, для выполнения которых на протяжении любого данного календарного периода необходима трудовая (учебная) деятельность одного работника СО или студента в течение полного (установленного законом) рабочего (учебного) времени за этот период, причем совокупность этих функций берется вместе с соответствующим обеспечением этих функций – материальным, энергетическим и информационным. Главным является понятие функции, выполняемой на РМ, а не его расположение в пространстве. Основной характеристикой РМ является показатель эффективности выполнения возложенных на него функций.
Рассмотрев группу работников СО, как развивающуюся систему (РС) [2,4,7-9], выделим две подсистемы: подсистему самосовершенствования А, в которой частью РМ работников СО создаются новые, более эффективные РМ работников СО (в результате самообучения), и подсистему B, в которой другой частью РМ работников СО выполняется внешняя функция системы – обучение студентов (при этом создаются РМ студентов). Каждой единице РМ работников СО (усредненной за единицу времени), появившейся в момент времени  , поставим в соответствие в момент времени
, поставим в соответствие в момент времени 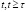 , два показателя ее эффективности (квалификации или технологии): функции
, два показателя ее эффективности (квалификации или технологии): функции 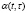 и
и  , характеризующие умения и способности единицы РМ работников СО, появившейся в момент
, характеризующие умения и способности единицы РМ работников СО, появившейся в момент  , в единицу времени, начиная с момента
, в единицу времени, начиная с момента  , производить в результате самообучения и обучения соответственно новые РМ работников СО и новые РМ студентов. Новыми РМ работников СО или студентов называются здесь такие РМ, для которых их показатели эффективности
, производить в результате самообучения и обучения соответственно новые РМ работников СО и новые РМ студентов. Новыми РМ работников СО или студентов называются здесь такие РМ, для которых их показатели эффективности 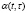 и
и 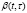 ,
, 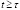 , не убывают с ростом
, не убывают с ростом  и не возрастают с ростом
и не возрастают с ростом  (например, возрастание по
(например, возрастание по  функции
функции  означает, что вследствие применения новых технологий самообучения РМ работников СО, появившиеся позже момента
означает, что вследствие применения новых технологий самообучения РМ работников СО, появившиеся позже момента  , обладают более высоким показателем эффективности по сравнению с РМ, появившимися в момент
, обладают более высоким показателем эффективности по сравнению с РМ, появившимися в момент  , а убывание по
, а убывание по  означает, что вследствие научно-технического прогресса РМ, появившиеся в момент
означает, что вследствие научно-технического прогресса РМ, появившиеся в момент  , с течением времени
, с течением времени  обладают все более низким показателем эффективности, т.е. технологически устаревают). Обозначим через
обладают все более низким показателем эффективности, т.е. технологически устаревают). Обозначим через 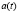 максимальный момент времени, ранее которого появившиеся в СО РМ работников СО не участвуют в производстве новых РМ в момент времени
максимальный момент времени, ранее которого появившиеся в СО РМ работников СО не участвуют в производстве новых РМ в момент времени  , т.е.
, т.е. 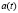 – временная граница ликвидации устаревших РМ в подсистеме А, начиная с момента
– временная граница ликвидации устаревших РМ в подсистеме А, начиная с момента  . Аналогично рассмотрим группу студентов как РС, в которой подсистемы А и B совпадают, так как новые более эффективные РМ студентов, появившиеся в результате самообучения студентов, и являются внешней функцией системы. Каждой единице РМ студентов (усредненной за единицу времени), появившейся в момент времени
. Аналогично рассмотрим группу студентов как РС, в которой подсистемы А и B совпадают, так как новые более эффективные РМ студентов, появившиеся в результате самообучения студентов, и являются внешней функцией системы. Каждой единице РМ студентов (усредненной за единицу времени), появившейся в момент времени  , поставим в соответствие в момент времени
, поставим в соответствие в момент времени 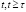 , показатель ее эффективности (квалификации или технологии) – функцию
, показатель ее эффективности (квалификации или технологии) – функцию 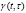 , характеризующую умения и способности единицы РМ студентов, появившейся в момент
, характеризующую умения и способности единицы РМ студентов, появившейся в момент  , в единицу времени, начиная с момента
, в единицу времени, начиная с момента  , производить в результате самообучения новые РМ студентов. Предлагаемые в работе уравнения, описывающие процесс самообучения студентов, являются более общими по сравнению с предложенными в [8], так как с добавлением в уравнения правых частей
, производить в результате самообучения новые РМ студентов. Предлагаемые в работе уравнения, описывающие процесс самообучения студентов, являются более общими по сравнению с предложенными в [8], так как с добавлением в уравнения правых частей 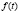 появляется возможность учета непосредственного воздействия внешних для рассматриваемого процесса факторов (например, в результате поступления извне нового более производительного информационного обеспечения процесса обучения появляются новые более эффективные РМ работников СО и студентов соответственно); кроме того, благодаря введению распределительной функции
появляется возможность учета непосредственного воздействия внешних для рассматриваемого процесса факторов (например, в результате поступления извне нового более производительного информационного обеспечения процесса обучения появляются новые более эффективные РМ работников СО и студентов соответственно); кроме того, благодаря введению распределительной функции 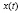 возможны постановки новых оптимизационных задач [2, с. 119-169]. Уравнения предлагаемой модели (их можно вывести аналогично [1]) имеют вид:
возможны постановки новых оптимизационных задач [2, с. 119-169]. Уравнения предлагаемой модели (их можно вывести аналогично [1]) имеют вид:
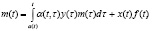
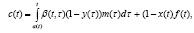
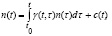
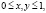
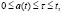
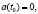
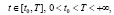
на начальном отрезке 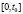 предполагается заданной начальная предыстория: функцию
предполагается заданной начальная предыстория: функцию 
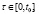 считаем заданной (известную на предыстории функцию обозначаем той же буквой с индексом «0»).
считаем заданной (известную на предыстории функцию обозначаем той же буквой с индексом «0»).
1. Положив
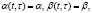
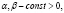
рассмотрим следующие уравнения модели:
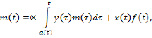
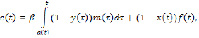
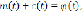
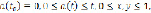
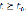 (1)
(1)
где 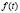 – скорость поступления извне внешнего ресурса в момент
– скорость поступления извне внешнего ресурса в момент 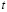 в СO,
в СO,  – скорость появления нового продукта первого рода (новых РМ работников СО) в момент времени
– скорость появления нового продукта первого рода (новых РМ работников СО) в момент времени  , выполняющего внутренние функции системы в подсистеме А; x(
, выполняющего внутренние функции системы в подсистеме А; x( ) и (1-x(
) и (1-x( )) – относительные доли
)) – относительные доли 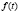 , поступающие в подсистемы A и B соответственно;
, поступающие в подсистемы A и B соответственно; 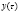 – доля продуктов
– доля продуктов 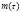 , идущих в момент
, идущих в момент  на воссоздание
на воссоздание 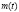 ;
;  – показатель эффективности создания продуктов, выполняющих внутренние функции системы: количество продуктов
– показатель эффективности создания продуктов, выполняющих внутренние функции системы: количество продуктов 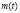 , создаваемых в единицу времени в расчете на единицу продуктов
, создаваемых в единицу времени в расчете на единицу продуктов 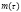 ,
, 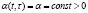 ;
; 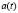 – временная граница ликвидации устаревших технологий создания продуктов первого и второго рода (другими словами, [
– временная граница ликвидации устаревших технологий создания продуктов первого и второго рода (другими словами, [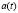 ,
, ] – временной промежуток, на котором создаются продукты первого и второго рода, используемые в момент времени
] – временной промежуток, на котором создаются продукты первого и второго рода, используемые в момент времени  , причем
, причем 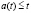 ;
; 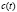 – скорость создания нового продукта второго рода (новых РМ студентов, появившихся в результате их обучения работниками СО) в момент времени
– скорость создания нового продукта второго рода (новых РМ студентов, появившихся в результате их обучения работниками СО) в момент времени  ;
; 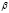 – показатель эффективности создания продуктов, выполняющих внешние функции системы: количество продуктов
– показатель эффективности создания продуктов, выполняющих внешние функции системы: количество продуктов 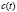 , создаваемых в единицу времени в расчете на единицу продуктов типа
, создаваемых в единицу времени в расчете на единицу продуктов типа 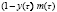 ,
,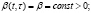
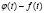 – скорость производства в момент t продуктов как первого, так и второго рода (эта скорость характеризует производственный потенциал системы).
– скорость производства в момент t продуктов как первого, так и второго рода (эта скорость характеризует производственный потенциал системы).
Будем считать, что процесс прогнозирования начинается с момента 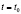 , причем для
, причем для 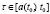 известна так называемая начальная предыстория или начальный ресурс системы: на этом временном отрезке предыстории
известна так называемая начальная предыстория или начальный ресурс системы: на этом временном отрезке предыстории  – заданная функция. Возможен случай отсутствия начальной предыстории, в этом случае РС называется возникающей [3].
– заданная функция. Возможен случай отсутствия начальной предыстории, в этом случае РС называется возникающей [3].
Положим y=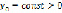 . Из уравнений (1) получаем
. Из уравнений (1) получаем


Обозначив 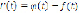 , получаем
, получаем
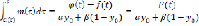 ,
,

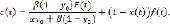
Вынужденные колебания здесь определяются поведением функций 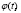
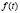 и
и 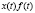 : если эти функции, определенные на общем множестве, являются периодическими функциями с соизмеримыми периодами, то m(t), c(t) являются периодическими (периоды
: если эти функции, определенные на общем множестве, являются периодическими функциями с соизмеримыми периодами, то m(t), c(t) являются периодическими (периоды 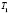 и
и 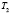 функций соответственно
функций соответственно 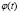 и
и 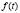 соизмеримы, если
соизмеримы, если 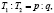 где
где 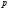 и
и 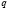 – взаимно простые числа, в этом случае число T = qT1 = qT2 есть период функций φ(t) ± f(t) и φ(t)f(t)) [5, с.59, задача 120].
– взаимно простые числа, в этом случае число T = qT1 = qT2 есть период функций φ(t) ± f(t) и φ(t)f(t)) [5, с.59, задача 120].
2. Определим собственные детерминированные колебания. Будем считать функции модели достаточное число раз дифференцируемыми по переменной  , заданными положительные константы α, β и функции
, заданными положительные константы α, β и функции 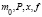 (в своих областях определений). Зададим функцию
(в своих областях определений). Зададим функцию  в виде:
в виде:
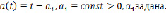 (2)
(2)
Тогда из (1) получим дифференциально-разностные уравнения запаздывающего типа [6]:
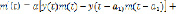
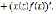
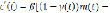
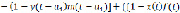 )
) ,
, 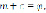
откуда
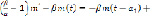
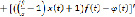 , (3)
, (3)
Если 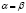 , то при помощи математической индукции нетрудно показать, что
, то при помощи математической индукции нетрудно показать, что
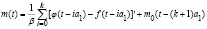 ,
,
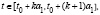
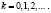 (4)
(4)
Если 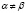 , то решая на каждом из отрезков
, то решая на каждом из отрезков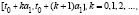 задачу Коши (например, методом Бернулли), получаем с помощью метода математической индукции
задачу Коши (например, методом Бернулли), получаем с помощью метода математической индукции
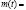
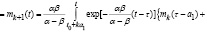
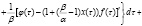
 (5)
(5)
Пологая в (4) и (5)
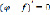 и
и 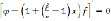 соответственно, получим
соответственно, получим
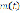
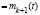
 , если
, если 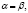
а при 
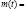

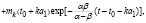
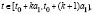
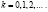
Следовательно, если 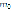 будет колебательной функцией, то и
будет колебательной функцией, то и 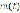 будет колебательной.
будет колебательной.
3. Рассмотрим аналогично [9, с. 262] случай, когда 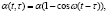
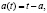
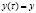 , где
, где 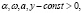 и уравнения модели имеют вид:
и уравнения модели имеют вид:
t = αyt–at (1 – cosω(t – τ))mτdτ + xtft,
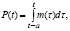
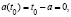
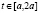 .
.
Предполагая функции модели достаточное число раз дифференцируемыми по переменной 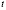 , все константы и функции
, все константы и функции 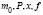 заданными в своих областях определений, получаем
заданными в своих областях определений, получаем
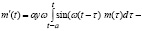

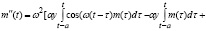

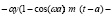
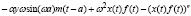
Т.о., для  получили обыкновенное линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
получили обыкновенное линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
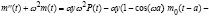
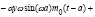
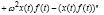 (6)
(6)
с начальными условиями:
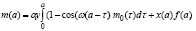

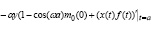 (7)
(7)
Характеристическое уравнение соответствующего однородного уравнения 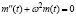 имеет вид:
имеет вид: 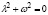 . Корнями последнего уравнения являются числа
. Корнями последнего уравнения являются числа 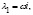
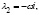 где
где 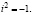 Следовательно, общее решение
Следовательно, общее решение 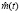 однородного уравнения записывается в виде
однородного уравнения записывается в виде 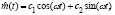
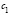 и
и 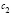 – const,
– const, 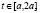
Это означает, что решение уравнения (6) есть довольно общая колебательная функция, зависящая от свободного члена уравнения (6) и начальных условий (7).
Очевидно, полученное на отрезке 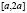 решение можно аналогично продолжить на отрезок
решение можно аналогично продолжить на отрезок 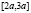 , … [ka, (k + 1)a],
, … [ka, (k + 1)a], 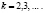
Выводы. Предложена интегральная модель системы образования, учитывающая процессы обучения и самообучения работников образования и студентов, а также непосредственное воздействие на систему образования внешней среды (например, другой системы образования). Получены периодические и колебательные решения дифференциально-разностных модельных уравнений запаздывающего типа. Полученные решения могут быть использованы при решении различных оптимизационных задач [1, с. 119-143]. Заметим, что если положить то получим результаты [4, с. 112-113] и [9, с. 262]. Для дальнейших исследований представляет интерес аналогичное [4, с.114-122] и [9, с. 263-266] изучение и других случаев колебательных режимов.
Библиографическая ссылка
Антонюк Ю.Ю., Гирлин С.К. ИНТЕГРАЛЬНАЯ МОДЕЛЬ СИСТЕМЫ ОБРАЗОВАНИЯ И КОЛЕБАТЕЛЬНЫЕ РЕШЕНИЯ ЕЕ УРАВНЕНИЙ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14103 (дата обращения: 21.11.2024).

