Согласно универсальной структурной классификации профессора Дворникова Л.Т. [1] все механизмы делятся на ассуровы и неассуровы. Ассуровыми называют механизмы, в которых ведущее звено или вращается относительно стойки, или движется относительно нее поступательно. По Ассуру все механизмы создаются от так называемого «простого кривошипа», т.е. от звена, соединенного со стойкой в одноподвижную кинематическую пару. При создании ассуровых механизмов к ведущему звену кривошипу или ползуну достаточно присоединять группы, обладающие нулевой подвижностью (ГНП). Синтез структур ассуровых трехзвенных механизмов сводится к поиску однозвенных ГНП [2].
Однако возможно создание неассуровых механизмов, т.е. таких в которых ведущие звенья связываются со стойкой в пары более высоких классов – р4, р3, р2, позволяющие две и более подвижности, при этом все подвижности кроме одной оказываются зависимыми.
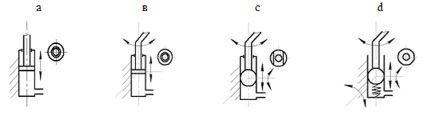
Так, если в отличие от известной конструкции поршня (рис. 1 ,а), в качестве ведущего звена использовать поршень гидроцилиндра с уголковым штоком (рис. 1 в), то входная пара окажется парой четвертого класса. В этом случае поршень обладает двумя движениями, а именно поступательным вдоль оси гидроцилиндра и вращательным, вокруг той же оси. Если поршень гидроцилиндра выполнить сферическим, то принципиально возможно на входе механизма организовать кинематические пары р3 (рис. 1 с) и р2 (рис. 1 d).
Для синтеза неасуровых механизмов воспользуемся уравнением W=Wпр+Wгр, где Wпр - подвижность привода; Wгр - подвижность присоединяемой группы; W – подвижность механизма.
Так при использовании известной конструкции поршня (рис. 1,а) Wпр=1, W=1, следовательно Wгр=0; при использовании поршня с двумя движениями (рис. 1 в) Wпр=2, W=1, Wгр=1; и при использовании поршня с четырьмя движениями (рис. 1 d) Wпр=4, W=1, Wгр=-3.
Для поиска групп воспользуемся универсальной структурной системой (1)
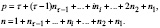(1)
В качестве начальных условий примем n=1, τ= 2, Wпр=2, Wгр=-1, W=1, т.к. будем рассматривать трехзвенные механизмы второго вида, тогда получим
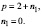(2)
Например, при использовании лишь пар p3 и p4 воспользуемся формулой подвижности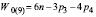 
, подставив в нее начальные значения, получим 
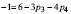, решая совместно с (2) получим, что в данной группе присутствуют одна пара p4 и одна пара p3. Этому решению удовлетворяет схема механизма, показанного на рис. 2.
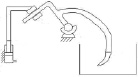
Рис. 2. Пространственный механизм с многоподвижным приводом
Аналогично можно найти все существующие схемы неассуровых механизмов (механизмов с многоподвижными приводами), которые могут быть использованы в различных областях техники и представляют интерес для детального изучения.
Библиографическая ссылка
Попугаев М.Г. ПРОСТРАНСТВЕННЫЕ МЕХАНИЗМЫ С МНОГОПОДВИЖНЫМИ ПРИВОДАМИ // Международный студенческий научный вестник. – 2015. – № 5-5. ;URL: https://eduherald.ru/ru/article/view?id=14069 (дата обращения: 24.04.2024).