В последние годы алгоритмы, заимствованные у природных систем, широко применяются в различных отраслях науки и техники. Это связано с тем, что природа за многие годы эволюции выработала действенные технологии оптимизации. Использование таких алгоритмов в решении задач дискретной оптимизации, позволяют находить оптимальные значения параметров объектов и структур. Одной из перспективных технологий является методы, основанные на роевых алгоритмах. Данные метод описывают коллективное поведение децентрализованной самоорганизующейся системы. Роевые алгоритмы впервые были предложены Херардо Бени и Ван Цзином в 1989 году [1]. Эти алгоритмы рассматривают самоорганизующуюся многоагентную систему. Агенты обычно довольно просты, но локально взаимодействуя вместе, создают так называемый роевой интеллект. Примерами таких систем в природе могут служить апроксимационные алгоритмы, относящиеся к классу метаэвристик, такие как:
– муравьиный алгоритм (Ant colony optimization);
– метод роя частиц (Particle swarm optimization);
– пчелиный алгоритм (Bees algorithm) и др.
Перечисленные выше алгоритмы были реализованы для решения различных NP-полных задач. Одна из наиболее известных задач комбинаторной оптимизации является задача коммивояжера, которая заключается в отыскании самого выгодного маршрута, проходящего через указанные города как минимум один раз с последующим возвратом в исходный город. Таким образом, коммивояжер сталкивается с задачей поиска гамильтонова контура минимальной длины в котором каждая вершина посещается только один раз.
Гамильтонов контур возможен только в связанном графе с четными степенями вершин. Поэтому, выполняется решение общей задачи коммивояжера, которая заключается в поиске минимального маршрута (минимальной протяженности, длительности и стоимости) с возвратом в исходную точку.
Сформулируем задачу в терминах теории графов. В неориентированном взвешенном графе G=(X,A), каждому ребру (xi, xj) которого сопоставлен вес L(xi,xj), требуется найти гамильтонов контур наименьшей стоимости, причем контур необязательно должен содержать все ребра графа. В условиях задачи указывается: критерии выгодности маршрута, матрицы расстояния, стоимости и т.п. Целью решения является нахождение маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат.
Решить поставленную задачу можно разными способами, которые отличаются точностью и скоростью решения. Наибольшую вычислительную трудоемкость имеют эвристические методы. Более приемлемыми являются метаэвристические методы. Преимущество метаэвристических методов перед классическими эвристическими, основанными на методе локального поиска, в том, что они позволяют исследовать большее пространство поиска для нахождения решения близкого оптимальному, тогда как методы локального поиска останавливаются после нахождения локального решения. В данной работе за основу взят «муравьиный» алгоритм. Привлекательность предложенного алгоритма в том что, хотя в его основе и лежит метод локального поиска, метод запретов позволяет продолжить поиск после нахождения локального оптимума, тем самым, расширяя пространство поиска, в надежде найти решение близкое к оптимальному [3].
Рассмотренные выше алгоритмы разрабатывались в рамках научного направления, которое можно назвать «природные вычисления». Исследования в этой области начались в середине 90-х годов XX века, автором идеи является Марко Дориго. В основе этой идеи лежит моделирование поведения колонии муравьев. Колония муравьев представляет собой систему с очень простыми правилами автономного проведения особей. Однако, несмотря на примитивность поведения каждого отдельного муравья, поведение всей колонии оказывается достаточно разумным. Основой поведения муравьиной колонии служит низкоуровневое взаимодействие, благодаря которому, в целом, колония представляет собой разумную многоагентную систему. Взаимодействие определяется через специальное химическое вещество – феромон, откладываемый муравьями на пройденном пути. При выборе направлении движения муравей исходит не только из желания пройти кратчайший путь, но и из опыта других муравьев, информацию о котором получает непосредственно через уровень феромонов на каждом пути. Концентрация феромона определяет желание особи выбрать тот или иной путь. Разработаны модификации муравьиного алгоритма, на основе которых получены более качественные решения для задачи поиска минимального гамильтонова цикла на тестах Эйлона для 50, 75 и 98 вершин. Для теста Эйлона с 30 вершинами оптимальное решение находится за 1-2 секунды [5].
Рассмотрим данный алгоритм на основе примера неориентированного нагруженного графа (рис. 1 а). Матрица весов дуг приведена на рис. 1 б. Матрица интенсивности феромона приведена на рис. 1 в. Требуется отыскать минимальный гамильтонов контур в графе. Начальная вершина x1.

а б в
Рис. 1. Пример поиска кратчайшего пути: а – граф; б – матрица весов дуг; в – матрица интенсивности феромона
Муравьиный алгоритм является итерационным. Каждая итерация состоит из следующих шагов:
Шаг 1. Для начала необходимо создать муравьев. Выбираем стартовую вершину xi, куда будут помещаться муравьи, зависит от ограничений, накладываемых условиями задачи. Потому что, для каждой задачи способ размещения является определяющим. «Муравьи» могут быть помещены в одну вершину, либо в разные с повторением, либо без повторении. На этом же шаге задается начальный уровень феромона, τij > 0 (рис. 1,в).
Шаг 2. Поиск решения. Находим вероятность перехода из вершины xi в вершину xj определяется по формуле 1.
 (1)
(1)
где Pij,k – функция вероятности перехода (где i – номер вершины в которой производится выбор, j – вершина, в которую должен направится муравей, k – номер муравья, движущегося по ребрам графа); τij – количество феромона, оставленного муравьями на ребре (хi,хj); ηij – величина, обратная весу (длине) ребра (хi,хj) (ηij =1/Lij, где Lij – расстояние между вершинами хi и хj ); α, β – эмпирические коэффициенты.
При α=0 выбор ближайшего города наиболее вероятен, т. е. алгоритм становится жадным. При β = 0 выбор происходит только на основании феромона, что приводит к субоптимальным решениям. Поэтому необходим компромисс между этими величинами, который находится экспериментально [6]. Принимаем значения α = 1, β = 2. Индекс m в сумме пробегает по всем не пройденным вершинам, смежным сi.
Важно отметить, что выбор пути производится не по максимуму функции Pij,k, а случайным образом с помощью генератора чисел, но на случай, конечно, влияет значение Pij,k. Рассмотрим на примере нашего графа (рис. 1 а).
После расчета вероятностей перехода из вершины x1 в вершины x2-x6, получаем отрезок (рулетка) с секторами вероятностей (рис. 2).
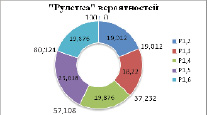
Рис. 2. Отрезок с секторами вероятностей
«Рулетка» вероятностей, размеченная функцией Pij,k, имеет неравные сектора. Чем ближе вершина и чем больше значение феромона, тем больше сектор. Таким образом, муравей использует и опыт предшественников τij, и здравый смысл ηij, и случайный фактор, т.е. все как в жизни [6]. Случайное число I1 = 75, полученное генератором случайных чисел попадает на 4 сектор. Этот сектор указывает на вершину 5. Далее муравей будет выбирать маршрут из этой вершины. Вершина 1 заносится в список запрещенных вершин (tabu list). Окончательное построенное дерево кратчайших путей состоит из дуг (рис. 3 е):
(х1,х5), (х5,х3), (х3,х4), (х4,х2), (х2,х6), (х6,х1)
Общая длина маршрута х1-х5-х3-х4-х2-х6-х1 имеет длину 19+19+19+14+8+11= 90.
Шаг 3. Обновление феромона. Уровень феромона обновляется в соответствии с формулой (2).
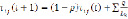 , (2)
, (2)
где ρ – интенсивность испарения, Lk (t) – цена текущего решения для k-го муравья, Q – параметр, имеющий значение порядка цены оптимального решения, т. е. Q/Lk(t)– феромон, откладываемый k-ым муравьём, использующим ребро (i,j).

Рис. 3. Текущие деревья кратчайшего пути – а, б, в, г, д и окончательное построенное дерево кратчайших путей – е
Для нахождения оптимального решения, в алгоритме муравья предусмотрено «испарение» феромона. Это достигается введением коэффициента ρ в итеративной формуле (2), применяющейся после каждого цикла обхода графа [6].
Заключение
В данной статье предложен новый механизм решения комбинаторных задач оптимизации, использующие математические методы, основанные на "природных" механизмах принятия решений. Основная идея, лежащая в основе алгоритма "муравьиной" колонии, заключается в использовании механизма положительной обратной связи, который помогает найти наилучшее приближенное решение NP-полной задачи.
Описанный в статье метод работает за несколько итераций и состоит из трех шагов. Ключевым моментом является то, что муравей выбирая путь из нескольких вершин учитывает опыт муравьев, которые прошли через эти вершины до него. Дойдя до определенной вершины, муравей выбирает из нескольких вершин следующую и прокладывает через нее свой путь. Если получившийся маршрут оказался "хорошим", тогда при следующей итерации такой выбор вершин будет более желательным.
Предложенный в статье подход для решения NP-полных задач является более эффективным по сравнению с существующими, а также позволяет вычислять более точные и подходящие маршруты при решении сложных задач.
Библиографическая ссылка
Юрлов А.А., Бурмистров А.В. РЕШЕНИЕ NP-ПОЛНЫХ ЗАДАЧ НА ОСНОВЕ МЕТОДА АДАПТИВНОГО ПОВЕДЕНИЯ МУРАВЬИНОЙ КОЛОНИИ // Международный студенческий научный вестник. – 2015. – № 3-2. ;URL: https://eduherald.ru/ru/article/view?id=12484 (дата обращения: 21.11.2024).

