Основным инструментом построения и сохранения необходимых пропорций в многоотраслевой экономике (да и в целом в народном хозяйстве) является балансовый метод и создаваемые на его основе различные балансовые модели [1].
Принципиальная схема многоотраслевого баланса производства и распределения совокупного продукта в стоимостном выражении может быть построена следующим образом.
Пусть рассматриваемая производственная сфера хозяйства состоит из n отраслей. Изучим их работу за некоторый промежуток времени (к примеру, за отчетный год). С этой целью введем следующие обозначения:
xi – общий (валовой) объем продукции i-й отрасли,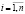 
;
xij – объем продукции i-й отрасли, потребляемой j-й отраслью при производстве объема продукции xj;
yi– объем продукции i-й отрасли, используемый в непроизводственной сфере (так называемый продукт конечного потребления).
Балансовый метод многоотраслевой связи состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов продукции, потребляемой производственной и непроизводственной сферах [2], то есть:
, 
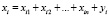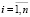. (1)
Данные уравнения называются соотношениями баланса.
Введя так называемые коэффициенты прямых материальных затрат по формуле:
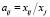, (2)
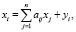
выражающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли, уравнения баланса можно записать в виде 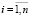[3]:
. (3)
или в более компактной (матричной) форме 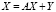[4]
, (4)
где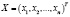 
– вектор валового продукта; 
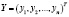– вектор конечного продукта; 
, 
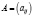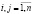– матрица прямых материальных затрат (технологическая или структурная матрица) [5].
Эти уравнения впервые получены и подробно изучены в 1936 г. американским ученым В. Леонтьевым, а позднее получили название уравнений межотраслевого баланса или линейной моделью Леонтьева.
Полученные уравнения баланса можно использовать в двух направлениях [6]:
1) либо по вектору конечного потребления определяют (планируют) величину валового выпуска;
2) либо по известному вектору валового выпуска Х находят вектор конечного потребления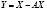 
.
Из перечисленных двух задач первая составляет основную задачу межотраслевого баланса.
В соответствии с экономическим смыслом параметров, входящих в уравнения (1), следует, что векторы Х, Y и матрица А должны быть положительными (т.е. должны быть положительны элементы, их составляющие: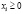 
; 
; 
, 
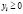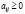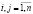) [8].
Рассматривая вопрос о разрешимости уравнения (4), сначала перепишем его в виде:
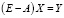. (5)
Если матрица E–A невырожденная, т.е. ее определитель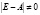 
, то это означает, что уравнение (5) имеет единственное решение [9]:
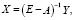(6)
где обратная матрица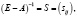 
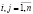называется матрицей полных материальных затрат [10]. Выясняя экономический смысл ее элементов, в качестве вектора конечного продукта Y возьмем последовательно единичные векторы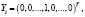 
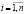, i-я координата которых равна единице. Им соответствуют векторы валового продукта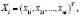 
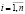. Следовательно, каждый элемент sij матрицы S выражает величину выпуска продукции i-й отрасли, необходимого для производства единицы конечного продукта j-й отрасли: 
, 
.
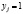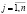Поскольку в дальнейшем нас будут интересовать только положительные решения уравнения (4), то укажем некоторые условия существования таких решений.
Матрица А с неотрицательными элементами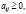 
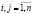называется продуктивной, если для 
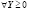существует положительное решение 
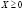. В этом случае и модель Леонтьева также называется продуктивной [11].
Следующие теоремы выражают достаточные условия продуктивности модели Леонтьева.
Теорема 1. Если для матрицы А с положительными элементами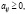 
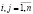и некоторого 
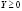уравнение (4) имеет положительное решение 
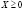, то матрица продуктивна.
Теорема 2. Матрица А с положительными элементами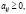 
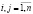продуктивна, если:
1) 
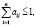
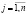
2) хотя бы для одного из столбцов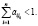 
Теорема 3. Для того чтобы матрица А была продуктивной, необходимо, чтобы элементы матрицы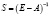 
были положительными, т.е.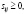 
Чтобы наглядно разобраться в вышеизложенном, рассмотрим конкретный пример.
В таблице приведены данные об исполнении баланса между двумя видами отраслей за некоторый период.
|
Отрасль |
Внутрипроизводственное потребление, ден. ед. |
Конечный продукт, xi |
Валовой продукт, yi |
|
|
Энергетика |
8 |
20 |
52 |
80 |
|
Машиностроение |
12 |
16 |
72 |
100 |
Необходимо вычислить:
1) величину конечного продукта, если вектор валового выпуска составил бы
;
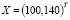2) необходимый объем выпуска отраслей, если объем конечного потребления увеличить до уровня
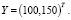
Сначала, используя данные таблицы и формулу (2), составим матрицу прямых затрат
и затем построим матрицу полных затрат
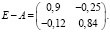
1) величину конечного продукта вычислим по формуле (5):
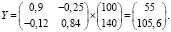
2) поскольку определитель матрицы
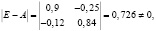
то эта матрица обратима следующим образом
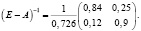
Из последней формулы следует, что все элементы матрицы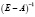 
положительны. Следовательно, согласно теореме 3 матрица А продуктивна и решение системы (5) положительно при любых значениях конечного продукта, в частности и при 
:
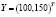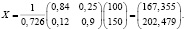
Таким образом, чтобы обеспечить конечный продукт в объеме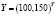 
, валовой выпуск в энергетической отрасли нужно поднять до 167,355 ден. ед., а в машиностроительной – до 202, 479 ден. ед.
Таким образом, метод Леонтьева отличает ясность и простота, универсальность и глобальность, другими словами пригодность для экономики отдельных стран и регионов, для мирового хозяйства в целом, следовательно, межотраслевой анализ может служить основным инструментом стратегического планирования [12].