В связи с успехами пленочной технологии выращивания железо-иттриевого граната (ЖИГ) появилась возможность применения спиновых и магнитоупругих (МУ) колебаний и волн в эпитаксиальных структурах, состоящих из пленок ЖИГ, выращенных на подложках гадалиний-галлиевого граната (ГГГ), для создания устройств аналоговой обработки сверхвысоко частотных (СВЧ) электромагнитных сигналов в реальном масштабе времени [1-5].
Вопросы взаимодействия обменных спиновых и упругих волн в перпендикулярно намагниченных пленках ЖИГ с любой толщиной пленки при определенных состояниях поверхностных спинов пленки рассмотрены в работах [1-5]. В настоящее время по нашему мнению представляет интерес рассмотрение взаимодействия обменных спиновых и упругих волн в касательно намагниченных тонких пластинах и эпитаксиальных пленках ЖИГ. Этот интерес обусловлен тем, что при касательном намагничивании пластины или пленки ЖИГ до насыщения требуется приложить достаточно меньшее по значению внешнее постоянное магнитное поле, чем при перпендикулярном их намагничивании.
Целью работы является теоретическое исследование спектра МУ колебаний в касательно намагниченных тонких пластинах и эпитаксиальных структурах ЖИГ-ГГГ в условиях взаимодействия обменных спиновых и упругих волн при учете обменных граничных условий, выражающих произвольные состояния поверхностных спинов тонких пластин и плёнок ЖИГ.
Полная энергия феррита, при учете МУ связи, состоит из магнитной, обменной, упругой и МУ энергии. Динамику феррита в рамках феноменологического подхода описывают связанные уравнения прецессии намагниченности (уравнение Ландау-Лифшица [3,6]) и движения вектора упругого смещения. Решение этих уравнений должны удовлетворять обменным и упругим граничным условиям. Эти уравнения будем записывать и преобразовывать так, как в [2,4-7].
Рассмотрим тонкую пластину или пленку ЖИГ толщиной S в постоянном магнитном поле 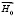 направленном вдоль оси z, которая паралельна поверхности пленки (рис. 1.3). Для случая распространения МУ волн в направлении x, которое совпадает с направлением кристаллографической оси III кубического кристалла, если учесть обменное взаимодействие, пренебрегая диполь-дипольным и принять, что упругие свойства ЖИГ и ГГГ являются изотропными, можно получить следующие линеаризованные уравнения движения:
направленном вдоль оси z, которая паралельна поверхности пленки (рис. 1.3). Для случая распространения МУ волн в направлении x, которое совпадает с направлением кристаллографической оси III кубического кристалла, если учесть обменное взаимодействие, пренебрегая диполь-дипольным и принять, что упругие свойства ЖИГ и ГГГ являются изотропными, можно получить следующие линеаризованные уравнения движения:
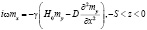 (1)
(1)
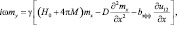 (2)
(2)
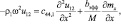 (3)
(3)
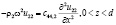 , (4)
, (4)
где mx и my – проекции переменной намагниченности на соответствующие оси координат (рис. 1), u12 и u22 – проекции упругого смещения на ось z для ЖИГ и ГГГ соответственно.
Уравнения (1) – (3) можно объединить в одно дифференциальное уравнение для переменной намагниченности mx:
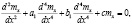 (5)
(5)
где введены следующие обозначения:
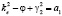 ; (7)
; (7)
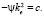 (8)
(8)
Здесь
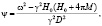
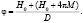
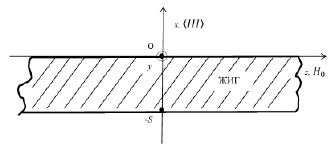
Рис. 1. Пластина ЖИГ, намагниченная касательно поверхности
Корни характеристического уравнения дифференциального уравнения (5) можно представить в виде:
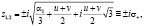 . (9)
. (9)
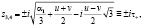 (10)
(10)
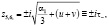 (11)
(11)
где 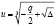 и
и 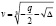 (кубические корни выбираються так, что
(кубические корни выбираються так, что  ).
).
Здесь
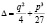 ,
,
где 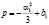 , а
, а 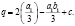 В отсутствие МУ связи, то есть когда
В отсутствие МУ связи, то есть когда 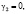 выражение (11) показывает, что могут существовать две поперечные линейно поляризованные упругие волны, каждая из которых может распространяться в положительном и отрицательном направлении оси x, то есть
выражение (11) показывает, что могут существовать две поперечные линейно поляризованные упругие волны, каждая из которых может распространяться в положительном и отрицательном направлении оси x, то есть 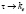 . Что касается выражений (9) и (10), то они определяют в этом случае, волновые вектора
. Что касается выражений (9) и (10), то они определяют в этом случае, волновые вектора 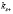 и
и 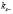 спиновой обменной волны частоты w:
спиновой обменной волны частоты w:
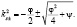 (12)
(12)
Из (12) видно, что значения 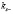 всегда чисто мнимые. Что касается значения
всегда чисто мнимые. Что касается значения 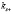 , то они являются мнимыми при
, то они являются мнимыми при 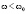 , где
, где 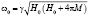 и действительными при
и действительными при 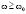 .
.
Решения уравнений (1) – (4) для случая 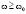 можно представить в виде:
можно представить в виде:
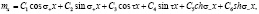 (14)
(14)
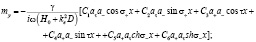 (15)
(15)
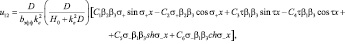 (16)
(16)
где 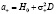 ,
, 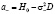 ,
, 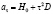 ,
, 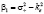 ,
,
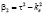 и
и 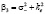 .
.
Будем рассматривать граничные условия в том случае, когда ось поверхностной анизотропии перпендикулярна поверхности пленки, так как обычно в пленках ЖИГ реализуется именно такой вид поверхностной анизотропии:
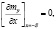 (17)
(17)
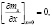 (18)
(18)
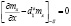 , (19)
, (19)
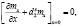 (20)
(20)
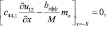 (21)
(21)
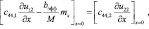 (22)
(22)
Подставляя решения (13) – (16) в граничные условия (17) – (24) и исключая постоянные 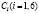 , найдем уравнение, которое определяет возможные значения
, найдем уравнение, которое определяет возможные значения 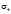 ,
, 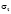 ,
, 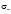 при произвольных параметрах закрепления поверхностных спинов
при произвольных параметрах закрепления поверхностных спинов 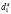 и
и 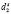 :
:
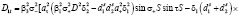
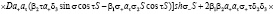
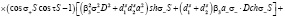
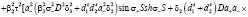
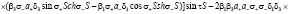
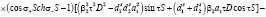
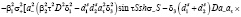
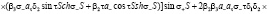
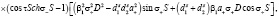 (25)
(25)
где 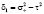 ,
, 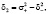
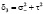 .
.
Анализируя уравнение (25) можно заметить что в пренебрежении МУ связью, то есть когда 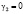 , уравнение (25) дает выражение для определения возможных значений
, уравнение (25) дает выражение для определения возможных значений 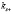 и
и 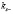 при произвольном закреплении поверхностных спинов тонкой пластины и пленки ЖИГ и выражение для определения возможных значений ke тонкой пластины и пленки ЖИГ.
при произвольном закреплении поверхностных спинов тонкой пластины и пленки ЖИГ и выражение для определения возможных значений ke тонкой пластины и пленки ЖИГ.
Далее рассмотрим спектр магнитоупругих колебаний в касательно намагниченных эпитаксиальных пленках ЖИГ в условиях спин-волнового резонанса.
Итак, рассмотрим эпитаксиальную пленку ЖИГ толщиной S выращенную на подложке ГГГ толщиной d в постоянном магнитном поле 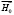 , направленном вдоль оси z, которая паралельна поверхности пленки (рис. 2). Для случая распространения МУ волн в направлении x, котрое совпадает с направлением кристаллографической оси III кубического кристалла, если учесть обменное взаимодействие, пренебрегая диполь-дипольным и принять, что упругие свойства ЖИГ и ГГГ являются изотропными, можно получить следующие линеаризованные уравнения движения (1) – (4), где mx и my – проекции переменной намагниченности на соответствующие оси координат (рис. 2), u12 и u22 – проекции упругого смещения на ось z для ЖИГ и ГГГ соответственно.
, направленном вдоль оси z, которая паралельна поверхности пленки (рис. 2). Для случая распространения МУ волн в направлении x, котрое совпадает с направлением кристаллографической оси III кубического кристалла, если учесть обменное взаимодействие, пренебрегая диполь-дипольным и принять, что упругие свойства ЖИГ и ГГГ являются изотропными, можно получить следующие линеаризованные уравнения движения (1) – (4), где mx и my – проекции переменной намагниченности на соответствующие оси координат (рис. 2), u12 и u22 – проекции упругого смещения на ось z для ЖИГ и ГГГ соответственно.
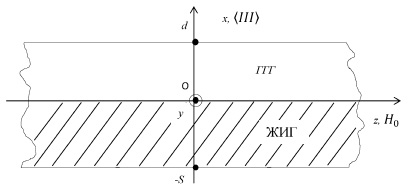
Рис. 2. Эпитаксиальная пленка ЖИГ, намагниченная касательно поверхности
Уравнения (1) – (3) можно объединить в одно дифференциальное уравнение для переменной намагниченности mx (5).
Корни характеристического уравнения дифференциального уравнения (5) можно представить в виде формул (9) – (11).
В отсутствие МУ связи, то есть когда 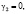 выражение (11) показывает, что могут существовать две поперечные линейно поляризованные упругие волны, каждая из которых может распространяться в положительном и отрицательном направлении оси x, то есть
выражение (11) показывает, что могут существовать две поперечные линейно поляризованные упругие волны, каждая из которых может распространяться в положительном и отрицательном направлении оси x, то есть 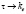 . Что касается выражений (9) и (10), то они определяют в этом случае, волновые вектора
. Что касается выражений (9) и (10), то они определяют в этом случае, волновые вектора 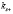 и
и 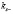 спиновой обменной волны частоты w по формуле (12).
спиновой обменной волны частоты w по формуле (12).
Из (12) видно, что значения 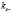 всегда чисто мнимые. Что касается значения
всегда чисто мнимые. Что касается значения 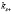 , то они являются мнимыми при
, то они являются мнимыми при 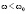 , где
, где 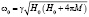 . и действительными при
. и действительными при 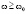 .
.
Решения уравнений (1) – (4) для случая 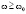 можно представить в виде формул (13) – (15) в области
можно представить в виде формул (13) – (15) в области 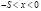 и
и
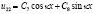 (26)
(26)
где 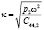 – величина волнового вектора упругой волны в ГГГ, где
– величина волнового вектора упругой волны в ГГГ, где 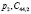 – плотность ГГГ и упругая постоянная ГГГ соответсвенно.
– плотность ГГГ и упругая постоянная ГГГ соответсвенно.
Будем рассматривать граничные условия в том случае, когда ось поверхностной анизотропии перпендикулярна поверхности пленки, так как обычно в пленках ЖИГ реализуется именно такой вид поверхностной анизотропии, по формулам (17) – (22),
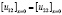 , (27)
, (27)
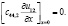 (28)
(28)
Подставляя решения (13) – (16) в граничные условия (17) – (24) и исключая постоянные 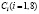 , найдем уравнение, которое определяет возможные значения
, найдем уравнение, которое определяет возможные значения 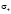 ,
, 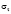 ,
, 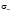 при произвольных параметрах закрепления поверхностных спинов
при произвольных параметрах закрепления поверхностных спинов 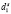 и
и 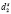 :
:
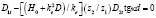 , (29)
, (29)
где D1t определяется выражением (25) и представляет собой уравнение дисперсии для пленки ЖИГ без подложки ГГГ:
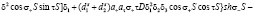
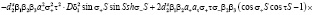
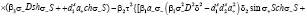
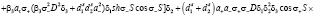
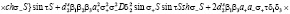
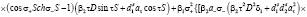
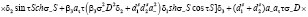
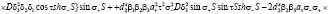
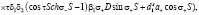 (28)
(28)
где 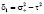 ,
, 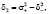
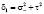 .
.
Анализируя уравнение (25), можно заметить, что в пренебрежении МУ связью, то есть когда 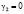 , уравнение (25) дает выражение для определения возможных значений
, уравнение (25) дает выражение для определения возможных значений 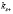 и
и 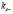 при произвольном закреплении поверхностных спинов эпитакксиальной пленки ЖИГ и выражение для определения возможных значений ke эпитаксиальной пленки ЖИГ [2,7].
при произвольном закреплении поверхностных спинов эпитакксиальной пленки ЖИГ и выражение для определения возможных значений ke эпитаксиальной пленки ЖИГ [2,7].
На основании уравнения (25) проведен численный расчет спектра частот МУ колебаний эпитаксиальной структуры ЖИГ – ГГГ при следующих параметрах пленки ЖИГ и подложки ГГГ [6,8]:
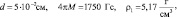
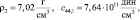
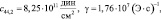
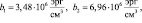
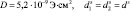 .
.
Величину подмагничивающего магнитного поля 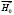 , в данном случае, следует принять равной 687,5 Э.
, в данном случае, следует принять равной 687,5 Э.
В таблице приведены результаты расчета для первых восьми МУ мод (отсчет ведется от частоты однородного ФМР) вблизи первой моды СВР пленки ЖИГ толщиной S=1 мкм при различных степенях закрепления поверхностных спинов. Приведенные результаты показывают, что в качественном отношении характер спектра и зависимость спектра от величины закрепления поверхностных спинов и толщины пленки оказывается в общем, такими же, как при перпендикулярной ориентации поля 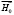 .
.
Результаты расчета для первых восьми МУ мод вблизи первой моды СВР пленки ЖИГ
|
ds см-1 |
Частоты МУ колебаний структуры ЖИГ- ГГГ, МГц |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
0 |
1925,821 |
1929,259 |
1932,759 |
1936,259 |
1941,665 |
1950,540 |
1954,063 |
|
1,0·103 |
1925,821 |
1929,250 |
1932,754 |
1936,247 |
1941,662 |
1950,541 |
1954,165 |
|
1,0·105 |
1925,696 |
1929,165 |
1931,853 |
1933,072 |
1936,259 |
1939,790 |
1943,321 |
|
1,0·107 |
1925,654 |
1929,124 |
1931,812 |
1933,030 |
1936,218 |
1939,750 |
1943,319 |
|
∞ |
1925,654 |
1929,124 |
1931,812 |
1933,030 |
1936,218 |
1939,750 |
1943,319 |
Выводы. В данной работе теоретически исследован спектр МУ колебаний, обусловленный взаимодействием обменных спиновых и уругих волн в продольно намагиниченной структуре ЖИГ – ГГГ. Показано, что характер такого спектра, зависимость спектра от величены закрепления поверхностных спинов и толщены пленки оказываются в общем, такими же, как при перпендикулярной ориентации постоянного магнитного поля.
Результаты данной работы могут быть использованы и частично уже используются в лаболатории функциональной электроники факультета радиофизики, электроники и компьютерных систем Киевского нациолального университета имени Тараса Шевченко для разработки ряда СВЧ-устройств, например, магнитострикционных преобразователей и линий содержки на их основе. Акт внедрения №052/178-15 от 14 декабря 2015 года

