Самостоятельный электрический разряд при низком давление газа, как правило, образовывается и при малом токе. Этот тлеющий разряд находит своё практическое применение в микроэлектронных технологических устройствах. Например, травление, виды источника света (лампы), напыление и т.д. [10]. Механизм преобразование света исходит от наличия у тлеющего разряда плазмы (положительного столбца). В этом состояние газ хороший проводник электричества, и тем самых на протяжении всего времени сохраняется высокая ионизация. В нынешнее время экономия занимает не мало важное место для людей и тем самым диффузионная обработка в тлеющем разряде является популярной темой для изучения. Она позволяет сэкономить расход электроэнергии и в большой степени технологический газ. Также к преимуществам использования тлеющего разряда можно привести наличие высокого коэффициента применения электроэнергии, сокращение по времени продолжительности процесса благодаря нагреванию тела до необходимой температуры насыщения, тем самым увеличивается активность газовой среды и поверхности катода [7]. Когда разрядный ток достигает порядка 1 А, то тлеющий разряд в газе атмосферного давления как правило сжимается в пятно, радиус которого равен приблизительно 1 миллиметра, что соответствует его нормальному режиму. В результате происходит рост температуры газа у катода, что привело к частичному уменьшению концентрации и у разрядного тока нормальной плотности, но к росту радиуса пятна. И это все происходит после непосредственного зажигания разряда. Во многих работах проведены исследования как экспериментального, так и теоретического характера при изучении изменений разряда и температуры в промежуточном катодном слое газа нормального тлеющего разряда атмосферного давления и поверхностного слоя в стабильном состоянии разряда.
В данной работе было рассчитано температурное изменение во времени в протяжённом цилиндрическом катоде при наличии пятна после зажигания самоподдерживающего нормального электрического разряда с холодным электродом в газе атмосферного давления (на этапе установления). Решена система уравнений, которая связывает среднюю температуру поверхность пятна и слоя тлеющего разряда, и тем самым обнаружена зависимость данных величин от промежутка времени.
Построим математическую модель. Пусть дан электрод, который будет выполнять в газовом разряде функции катода, где R- радиус цилиндра; L- длина цилиндра;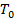 
-начальная температура. После того как зажгли нормальный тлеющий разряд, где t=0 – начальный момент времени, сформировалось катодное пятно тлеющего разряда с радиусом
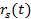в середине 1-ого из торцов (рисунок 1).
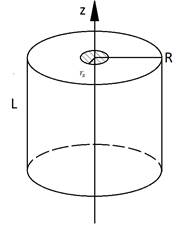
Рисунок 1. Геометрия электрода с пятном.
Предположим, что ось симметрии цилиндрической системы координат будет совпадать с осью электрода, а также направленной в разрядный объем от симметричной поверхности катода, находящемся рядом с пятном в плоскости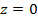 
. В результате движение электрических зарядов в катодном слое разряда в пятне, а точнее на поверхности электрода, падает однородный тепловой поток, который нагревает его, где плотность составляет
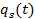; температура нижнего электродного торца также равна 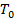; плоскость, где расположен и где происходит отвод тепла 
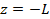. Тепловой поток его боковой поверхности пренебрежительно мал, из-за того, что теплопроводность газа значительно меньше материала электрода, и следовательно его можно опустить. Также наличие холодных электронов можно пренебречь, так как он не вызывает большого изменения на общей тепловой баланс, обусловленное тем, что имеется тепловое излучение с электродной поверхности. Следовательно, нестационарное уравнение теплопроводности будет описывать изменение с течением времени температуры электрона:
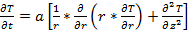(1)
Также имеются ограничения на торцах
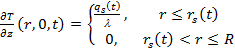, (2)
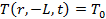, (3)
Поверхность боковая:
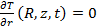, (4)
начальные условия:
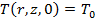, (5)
Элементы, которые будут не зависеть от изменения температуры:
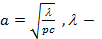коэффициент теплопроводности, 
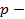плотность электрода, 
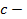удельная теплоёмкость материала электрода.
Данная краевая задача мот быть решена при помощи конечных интегральных преобразований Ханкеля и Фурьеи [1] и будет выглядеть следующим образом:
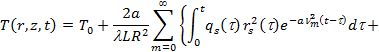
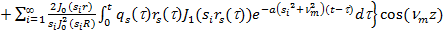. (6)
где 
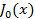и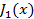 
- это функции 1-ого рода нулевого и 1-ого порядка Бесселя, 
, 
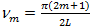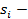является корнем уравнением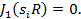 
Из (6) уравнения можем найти в пятне значение средней температуры:
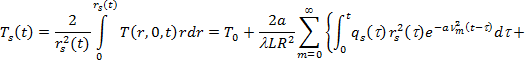
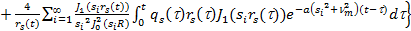. (7)
Из-за того, что радиус пятна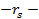 
намного больше ширины катодного слоя разряда 
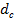, то в нём температура данного газа будет = 
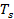. Большая часть тепловой мощности, которая выделяется в катодном тёмном пространстве разряда, через пятно переходит в катод, при плотности теплого потока:
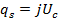, (8)
Нормальная плотность тока это j,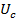 
- это падения напряжения разряда.
Так как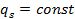 
по его сечению, то
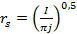, (9)
где I это разрядный ток.
Уравнения слоя тлеющего разряда определяют значения [8]:
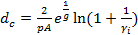(10)
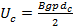, (11)
а у разрядного тока плотность будет составлять:
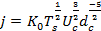, (12)
при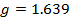 
, A и B – являются const для газа, представленного в данной работе, и которые входят в формулу зависимости коэффициента ионизации газа электронами от напряжённости электрического поля [6], 
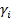– у материала катода является коэффициентом ионно-электронной эмиссии.
,
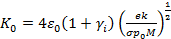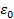- диэлектрическая постоянная, 
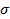- в газе является резонансной перезарядкой иона, e – иона заряд, M – иона масса, k - постоянная Больцмана.
Вследствие применения давления газа «p» будет происходить уменьшение концентрации газа впоследствии повышения его температуры (нагревания):
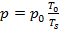, (13)
где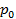 
это давление при соответствующей ему температуры 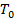в газе.
Уравнения с (7) по (13) составляют систему, причём замкнутую, которая описывает изменение в пятне средней температуры на поверхности катода, а также параметры разряда в катодном слое после того, как произошло зажигание разряда, с течением времени. Если исключить из этой системы такие величины, как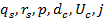 
, то получится уравнение вида:
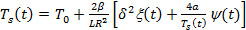, (14)
При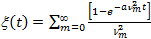 
,
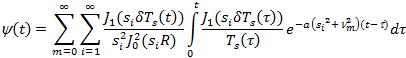
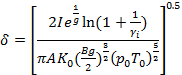
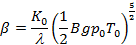
Данное решение можно получить численно. При переходе к пределу, где t®∞, мы получим уравнение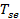 
. При чём следует отметить, что данная температура будет стремиться принять своё стационарное значения, т.е. 
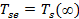, где интеграл будет вычисляться по t, а ряд суммироваться по m, вследствие получим :
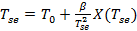, (15)
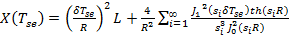(16)
Если считать, что радиус пятна будет намного меньше самих размеров электрода, т.е. R®∞, L®∞, то сумма в уравнение (16) преобразуется в интеграл [9], после вычисления которого из (23) получим выражение для получения в пятне ср. температуры на электроде, который в свою очередь занимает полупространство «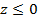
». Это все и доказывает, что выражения (14) и (15) верны.
Вычисления находились на основе данных гелия атмосферного давления для разряда, который использует цилиндрический стальной электрод в качестве катода (нормальное атмосферное давление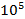 
Па, абсолютная температура 300К, сечение в гелии
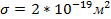, постоянные газа А и В соответственно
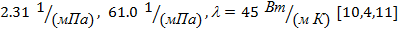). Исходя из выражения (15), была найдена 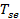в пятне для 2-х значений его радиуса, разрядный ток которого 1А, и установлена зависимость длины некоторого электрода 
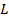от температуры на его поверхности (рисунок 2).
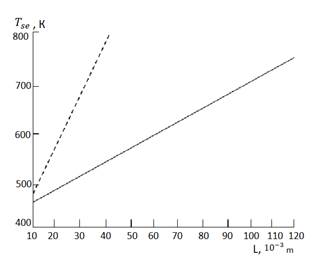
Рисунок 2. Установившаяся зависимость средней температуры от длины электрода.
Зависимость температуры от временипредставлена на рисунке 3, которая была получена при решении выражения (14) численным методом [2]. Анализируя рисунок 2 и 3, можно сделать вывод, что функция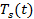 
принимает своё стационарное значения 460К, которое было достигнуто после нагревания его до 450К в течении 10 секунд.
В [4] работе было установлено в ходе эксперимента зависимость температуры от времени на поверхности электрода, радиус которого = 0,018 метров и длинны = 0,01 метра, при нагревании разряда в пятне. Можно заметить, что своего стационарного состояния она достигает к 750 К, пройдя промежуток времени равный 200 секунд. Однако, просматривая рисунок 2, видно, что для данного электрода такого же радиуса и такой же температуры он достигает при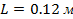 
. Это происходит из-за того, что в экспериментальной работе отвод тепла значительно затрудняется от электрода из-за того, что он осуществляется через его детали крепления, так как он нагревания до красноты при разрядном токе = 2А. В следствии чего не было выполнено граничное условие из-за нагревания у электрода нижнего торца. Это условие (3). Делаем вывод о том, что выражения (14)-(15) будем использовать при разрядном токе, который намного ниже представленного в данной работе, то есть до 0,3. Если же наоборот (для охлаждённого), то уравнение (3) будет верно тогда, когда разрядный ток будет намного выше, то есть при длине электрона = 0,0025 метров и разрядного тока = 1А средняя температура катода в представленной работе, которая рассчитана из (15) формулы и равна 410 К, будет совпадать в пятне 430 К.
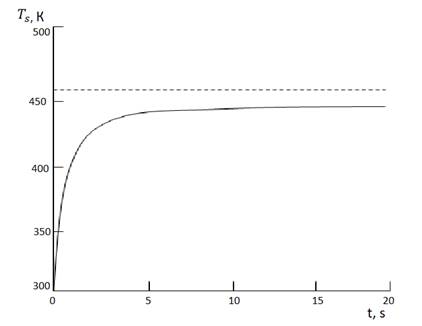
Рисунок 3. Зависимость средней температуры от времени горения разряда.
В работе было рассчитано температурное изменение во времени в протяжённом цилиндрическом электроде при наличии катодного пятна самоподдерживающего электрического разряда с холодным электродом в газе на его торцах после того, как зажгли нормальный тлеющий разряд при атмосферном давление. Учитывая, как влияет нагретый газ на поверхности пятна на его размер, найдено для нестационарного уравнения аналитическое решение, а также выведено выражение для нахождения значения средней температуры на поверхности в пятне электрода. Было найдено уравнение для постоянной во времени средней температуры 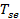поверхности в пятне электрода, впоследствии длительного горения разряда во времени.
При сравнивании полученных результатов расчётов и экспериментальных данных [5] в работt было найдено, что если использовать стальной катод, при наличии охлажденного нижнего торца выражения для нахождений 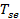, то справедливо при разрядного тока ≤ 1 А. Если же в случае когда нижней торец не охлаждён, то 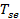будет меньше, чем в предложенном эксперименте, при I> 0.3. Это происходит из-за того, что используется при его выводе предположение о том, что была фиксирована температура у электрода на нижнем торце, который не выполняется в таких условиях.
Библиографическая ссылка
Однорожникова С.И., Торшина О.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕПЛООБМЕНА В ЦИЛИНДРИЧЕСКОМ КАТОДЕ // Международный студенческий научный вестник. – 2018. – № 6. ;URL: https://eduherald.ru/ru/article/view?id=19409 (дата обращения: 20.04.2024).