В данной статье будет рассмотреназадача теплообмена между струей с большим показателем температуры и пластиной, внешняя поверхность которой подвержена воздействию двухфазной или однофазной струис начальными данными. Рассмотрим данную задачу с физической стороны[1]. Схема взаимодействия сверх высокотемпературной струи с преградой представлена на рисунке 1, где x – ось абсцисс, y– ось ординат; Lx – ширина пластины; Ly– толщина пластины; lg - длина воздействия струи; Qg – поток с высокой температурой; A, B, C, D, E– граничные точки. Сконструируем математическую модель теплообмена между струейc высокой температурой и пластиной [3]. Произведем числовое решение данной задачи.
При решении данной задачи не будем принимать во внимание:
1) допустимые процессы окисления и плавления материала преграды активными компонентами газового потока;
2) радиационная составляющая в теплообмен;
3) вложение радиационной составляющей в теплообмене на внешние плоскости;
4) характеристики теплофизике (λ, ρ, с), которые являются постоянными.
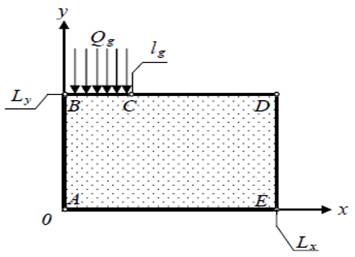
Рисунок 1 Область решения задачи
Математическое моделированиевключает в свой состав двумерное нестационарное уравнение теплопроводности, с соответствующими начальными и предельными критериями [5]
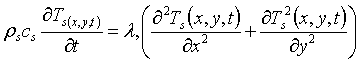 , (1)
, (1)
с первоначальным критерием:
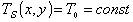 (2)
(2)
и предельными критериями:
– критерий теплообмена газового потока с поверхностью конструкционного материала:
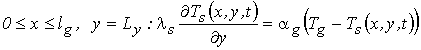 (3)
(3)
– критерий симметрии на вертикальной оси ординат:
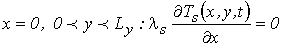 (4)
(4)
– критерий теплообмена с воздухом на боковой плоскости:
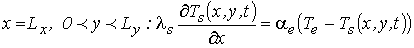 (5)
(5)
– критерий теплообмена с воздухом на противоположной стороне пластины:
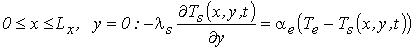 (6)
(6)
– критерийтеплообмена с воздухом на нагреваемой плоскости [6]:
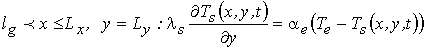 (7)
(7)
где ρ – плотность; T - температура; t – время; α – коэффициент теплообмена; с – коэффициент удельной теплоемкости; λ – коэффициент теплопроводности.
При числовом решении задачи (1) – (7) обратимся к методуРекфорда – Писмена [4]. Для аппроксимации дифференциального уравнения (1) разностным методом детерминируем пространственно-временную сетку [2] с координатами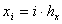 ;
; 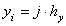 ,
, 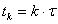 , где
, где 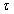 – шаг по времени;
– шаг по времени; 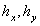 – шаги на плоскости;
– шаги на плоскости; 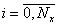 ,
, 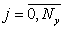 и
и 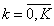 . В конечном итоге,вся проектируемая область покрывается сеткой (рис.2).
. В конечном итоге,вся проектируемая область покрывается сеткой (рис.2).
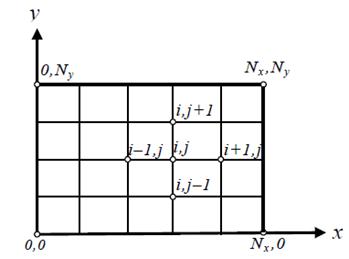
Рисунок 2 Разностная сетка области решения
Дискретизацию уравнения (1) реализуем при помощи локально-одномерной схемы А.А. Самарского, которая характеризуется свойством суммарной аппроксимации и является полностью устойчивой. Введем обозначения: 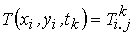 . Основная идея метода [9] сводиться к тому, что шаг по времени изменяется в два этапа. На промежуточном временном шаге выполняется дискретизация двумерного уравнения (1) по направлению оси абсцисс и следовательно, получается одномерное уравнение. После этого сновапроизводимдискретизацию уравнения (1), но уже в направлении оси ординат. При решении полученных одномерныхуравнений, установим поле температуры на шаге по времени [6].
. Основная идея метода [9] сводиться к тому, что шаг по времени изменяется в два этапа. На промежуточном временном шаге выполняется дискретизация двумерного уравнения (1) по направлению оси абсцисс и следовательно, получается одномерное уравнение. После этого сновапроизводимдискретизацию уравнения (1), но уже в направлении оси ординат. При решении полученных одномерныхуравнений, установим поле температуры на шаге по времени [6].
При использовании неявной схемы на каждом полушаге по времени, отобразим уравнение (1) в виде:
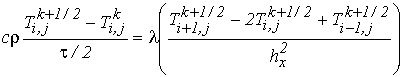 (8)
(8)
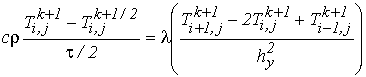 (9)
(9)
Аппроксимируя предельными критериями (2) - (7) получим:
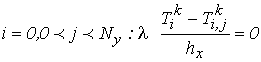 (10)
(10)
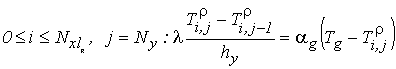 (11)
(11)
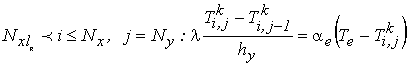 (12)
(12)
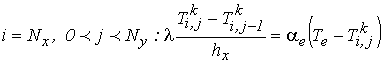 (13)
(13)
Разностные уравнения (8), (9) сводятся к стандартному трёх диагональному виду и решаются методом прогонки [8].
Приведем результаты вычислений при: Lx = 0,35 м, Ly = 0,25 м, lg=0,17 м, ρs = 1450 кг/м3; Ср = 770 Дж/(кг·ºK); λs = 1,3 Вт/(м·ºK); T0 = 200 ºК; Tg = 1800 ºК; Te = 200 ºК, αg = 3500 Вт/(м2·°С), αe = 50 Вт/(м2·°С). Результаты процесса нагрева пластины через 120 секунд приведены на рисунке 3.
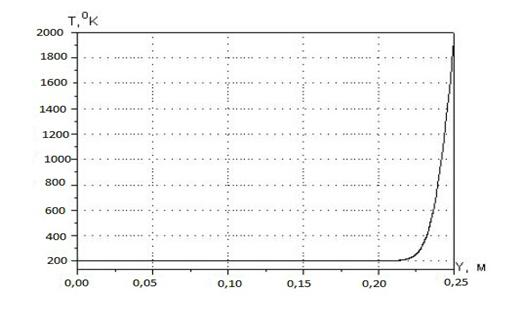
Рисунок 3 Процесс нагрева пластины
В данной статье уравнение (8) решается с помощью метода прогонки. Метод прогонки – легкий и продуктивный алгоритм, который решает системы линейных алгебраических уравнений с трехдиагональными матрицами. Приведем данное уравнение к виду [5]:
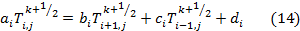
Преобразуем уравнение (8):
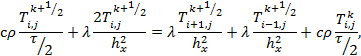
после
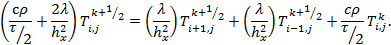
Отсюда получаем, что
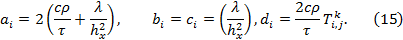
При границах (AB) и (CD) (см. рис. 2) для точек 0 и  будет записано в виде:
будет записано в виде:
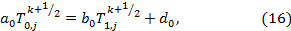
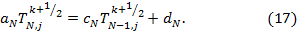
Выражения (16) и (17) будут рассматриваться в виде (14), при  , так как граничные точки имеют только по одной соседней точке.
, так как граничные точки имеют только по одной соседней точке.
Следует записать коэффициенты  , которые входят в (16) и (17), для осуществления граничных условий (10) и (13) на соответствующих границах:
, которые входят в (16) и (17), для осуществления граничных условий (10) и (13) на соответствующих границах:
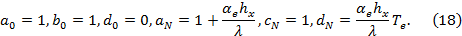
В записи уравнения (16) в виде возникает алгоритм прогонки:
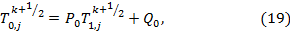
в котором,
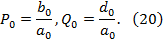
Соответствие (19) ставится в (14) для i=0. В конечном итоге получается, что из  можно выразить
можно выразить  . Продолжая процесс последовательной подстановки, из
. Продолжая процесс последовательной подстановки, из  можно выразить
можно выразить  :
:
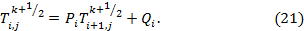
В этом случае,  – новые коэффициенты, которые появились в результате подстановки.
– новые коэффициенты, которые появились в результате подстановки.
Для того, чтобы выразить  необходимо вернуться на стадии процесса подстановок, когда выражали
необходимо вернуться на стадии процесса подстановок, когда выражали  в виде:
в виде:
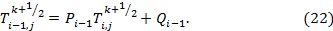
При подстановке (22) в (14) получаем выражение:
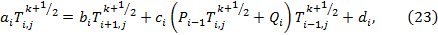
которое можно переписать в виде (21). Следовательно, получим  соответственно:
соответственно:
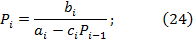
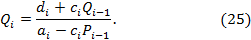
Таким образом, можно увидеть, что знаменатели в выражениях (24) и (25) одинаковые.
Выражения (24) и (25) рекурсивные, таким образом,  зависят от значений
зависят от значений  Данный рекурсивный процесс нуждается в отправной точке, которую обеспечивает выражением (20), которое не рекурсивно[3].
Данный рекурсивный процесс нуждается в отправной точке, которую обеспечивает выражением (20), которое не рекурсивно[3].
При переходе к вычислению  можно заметить, что, как и
можно заметить, что, как и  Таким образом, согласно (15)
Таким образом, согласно (15)  . Для того чтобы получить
. Для того чтобы получить  необходимо начать процесс обратной прогонки с использованием формулы (22)[3].
необходимо начать процесс обратной прогонки с использованием формулы (22)[3].
Запишем алгоритм для метода прогонки.
Алгоритм метода прогонки:
1. Из выражения (20) вычислим  .
.
2. При использовании рекурсивных формул (24) и (25) получим 
3. Будем считать, что 
4. Для того, чтобы найти  подставим найденные величины в формулу (22) для
подставим найденные величины в формулу (22) для  .
.
Алгоритм для решения уравнения (9) будет схожим. Граничные условия на границах (BC), (CD) и (AE) будут другими. Таким образом, коэффициенты  , которые входят в выражения (16) и (17) можно записать в следующем виде:
, которые входят в выражения (16) и (17) можно записать в следующем виде:
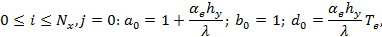
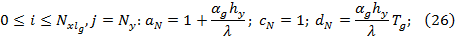
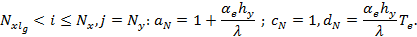
Коэффициенты  выражения (9), которые входят в уравнение (14) примут вид:
выражения (9), которые входят в уравнение (14) примут вид:
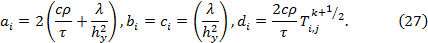
Прогонка будет выполняться по индексу j, неизвестными будут 
Полученные результаты могут быть использованы при решении задач рассмотренных в работе[10].
Библиографическая ссылка
Иванова Е.В., Торшина О.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕПЛООБМЕНА ПОСРЕДСТВАМ МЕТОДА РЕКФОРДА-ПИСМЕНА // Международный студенческий научный вестник. – 2018. – № 6. ;URL: https://eduherald.ru/ru/article/view?id=19371 (дата обращения: 20.04.2024).

