Введение
В нынешнее время в машиностроении и в любом производстве все более остро встает вопрос о модернизации и автоматизации используемого оборудования. В связи с этим становится актуальным применение высокопроизводительного технологического оборудования. Так как повышается сложность геометрической формы деталей и требований к точности и к качеству обрабатываемых поверхностей, и применением новых материалов. Ни для кого не секрет, что основная задача в области машиностроения является достижение высокой производительности при обработке материалов без потери в уровне качества. В настоящее время большими стремительными шагами развивается технологическое оборудование, использующее принципы мехатроники. Такое оборудование пользуется популярностью в различных объектах автоматизированной механической обработки и измерений. В принципах махатроники активно идет применение механизмов с параллельной кинематикой, при котором исполнительный инструмент (для механообработки) или измерительный инструмент (для измерительных мероприятий) может перемещаться по сложной траектории с помощью движения рабочего стола, на котором установлен инструмент. Перемещение стола происходит с помощью активных поступательных пар – приводов («штанг переменной длины» - винтовых механизмов), шарнирно соединенных со столом и основанием.
Классифицировать станки с параллельной кинематикой можно на две категории: манипуляторы с полной подвижностью (т.е. с шестью степенями свободы) и ограниченной подвижности (со степенями свободы равным пяти или менее). Последняя группа включает в себя манипуляторы, двигательные данные которых остаются неизменными во всем их рабочем пространстве. Примерами таких систем являются манипуляторы поступательного движения, сферические механизмы и роботы типа «SCARA» (рис.1).
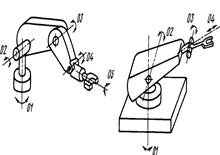
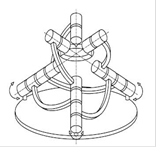
Рис. 1. Примеры параллельных манипуляторов первой группы
Однако в производстве существует потребность, чтобы инструмент менял свое положение и ориентацию в рабочем пространстве. Следовательно, тип движения должен иметь смешанные степени свободы. Такие манипуляторы вместе выполняют вращательные и поступательные степени свободы. В нынешнее время множество задач в области механической обработки требуют пятикоординатных операций, т.е. с двумя вращательными и тремя линейными степенями свободы. Основным недостатком пятикоординатных станков является их ограниченная статическая жесткость и ограничение по динамическим характеристикам. [6]
На начальном этапе одним из первых вариантов в области параллельной кинематики было использована архитектура, основанная на платформе Гью-Стюарта. В качестве примеров таких станков можно рассмотреть: «Variax», «Octahedral», «Mikromat 6X», «Cosmo Center PM-600» (на рис. 2 приведены некоторые из них).


Рис. 2. Станок с параллельной кинематикой Cosmo Center PM-600 и станок модели Mikromat 6X Hexa
Данные установки обладают лучшей жесткостью и динамическими характеристиками, чем станки с последовательной кинематикой. Тем не менее, существовало ограничение по диапазону вращательной подвижности и общему габаритному размеру. Для улучшения недостатков были выполнены другие параллельные установки, отличные от платформы Стюарта, такие как станок «Eclipse-RP» или «Metrom P1000» производства южнокорейской компании «Daeyoung Machinery» (рис.3). Не смотря, на это все еще существует проблема избыточного размера станка к отношению размеру рабочего пространства. [6]

Рис. 3. Станок P1000, его шпиндель и рабочая зона
Одним из вариантов уменьшения отношения размера станка к рабочему пространству является комбинирование последовательных кинематических модулей с параллельными модулями для основания гибридных установок. Примером гибридной кинематики является станок «Space 5H» ,который выпускает испанская компания «Fatronik». В станок установлен параллельный модуль (обрабатывающая головка «Hermes»), который соединен с рамой, имеющая две линейные степени свободы. Функционал станка разработан для сверления и фрезерования деталей в авиационной промышленности, но нет возможности обработать деталь с пяти сторон. Аналогичной машиной является станок «Ecospeed», который выпускается немецкой фирмой «DS Technologie». Из всех рассмотренных механизмов только гексаподы совмещают в себе все достоинства механизмов параллельной структуры.
Механизм гексапода наиболее распространенный и обеспечивает 6 степеней свободы. Он состоит из соединенных между собой шестью стойками фиксированной верхней платформой, которая имеет форму шестиугольника и подвижной треугольной платформы. К неподвижной платформе устанавливается при помощи шарниров каждая пара стоек и сходится вместе в общем шарнире, стоящий в одном из трех узлов подвижной опоры (рис.4).
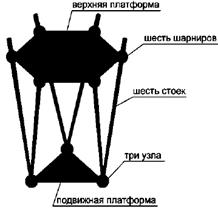
Рис. 4. Механизм гексапода
Передвижение подвижной опоры достигается за счет обобщенного между собой изменения длины стоек, а именно:
-когда все стойки в одно время удлиняются или уменьшаются с одинаковой скоростью, таким образом, платформа совершает движение вертикально в вверх или вниз при неизменном своем горизонтальном положении (рис. 5а).
-когда одни стойки увеличиваются, а другие, уменьшаются тем, самым меняют ориентацию, платформа движется в прямом направлении, до тех пределов пока не превысит разрешенное гексаподом горизонтальное перемещение (рис. 5б).
-когда происходят изменения длины и ориентации всех стоек, платформа имеет наклон относительно координатных осей, до предела, пока допустимый угол поворота не будет превышен (рис. 5в). [5]
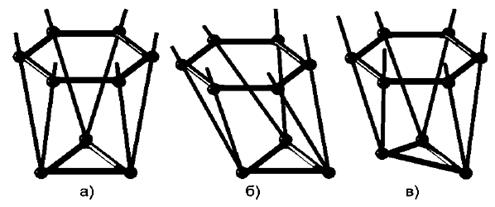
Рис. 5. модели движения гексапода
Можно утверждать, что вследствие осевых и угловых перемещений стоек подвижная платформа имеет возможность достичь любой точки рабочего пространства, на основании этого можно назвать гексапод отличным позиционирующим устройством.
Существует несколько вариаций в базовой конструкции гексаподов, которая различается используемым числом шарниров. Различные виды компоновок гексапода изображены на (рис. 6).

Рис. 6. Различные компоновки гексапода
Самая известная компоновка гексапода, как гексапод 6-6, представлен на рисунке 6 слева. Числу узлов, в которых стойки, крепятся с базовой платформой, соответствует первая цифра, аналогично вторая цифра обозначает число узлов, в которых стойки соединяются с рабочей платформой. В середине изображения показан гексапод 6-3, который характеризуется наличием шарниров, как на базовой платформе, так и в количестве трех шарниров на подвижной платформе. Справа показан гексапод 3-3, который собрал в себе по три шарнира на двух платформах.
Из множества достоинств, которые присуще гексаподам можно выделить следующие:
Шесть степеней свободы. Кроме ортогональных направлений X, Y, Z платформа совершает угловые перемещения (наклоны кручение).
Гибкость и приспособленность. Гексаподы могут работать непрерывно в соответствии с гибким производственным процессом. Под гибкостью понимается умение реагировать на запланированные изменения.
Производительность. Она повышается за счет непрерывной обработке, при которой происходит автоматическая смена заготовки, а так же при использовании высокоскоростного шпинделя и уменьшения массы подвижных деталей.
Жесткость и устойчивость. Имеют жесткий каркас, в котором отсутствуют деформации под нагрузкой.
Точность и надежность. Оценка точности осуществляется волюмометрической погрешностью. Нагрузки гексаподов преобразуются в растяжение или сжатие тем самым идет исключение изгибающих моментов, что сопутствует увеличению точности обработки.
Однако, несмотря на все преимущества, существует и ряд проблем, которые требуют улучшений. К основным ограничение гексаподов можно отнести:
Длина стоек. Из за возможной кривизны стоек, точность гексапода обратно пропорциональна их длине.
Температурные деформации. Значительные температурные деформации происходят из за быстрого перемещения стоек и также вследствие высокой скорости вращения шпинделя. [5]
Преимущества станков с параллельной кинематикой по сравнению с традиционными станками с прямоугольной системой координат видны невооруженном взглядом. Основным достоинством является высокоскоростная обработка, которая обеспечивает:
- уменьшение температуры обрабатываемой детали;
- получение более высокого класса шероховатости;
- в течение длительного времени сохранение точности обработки;
- увеличение подачи в 5-10 раз;
- уменьшение времени обработки на 40-70% и стоимости на 20-50%.
В сравнительной (табл. 1) показаны параметры механической обработки металла на традиционных станках и на установках с высокоскоростной обработкой.
Таблица 1. Сравнение параметров механической обработки
|
Механическая обработка на традиционных станках |
Механическая обработка на станках с параллельно кинематикой |
|
|
Частота вращения, |
6000 |
15-40000 |
|
Подача, м/мин |
0.2-0.8 |
1.5-5 |
|
Глубина резания, мм |
1-5 |
0.02-0.5 |
|
Твердость |
<36 |
<62 |
|
Сила резания |
высокая |
низкая |
|
Тепловыделение |
высокая |
малое |
Станки с параллельной кинематикой могут осуществить: окончательную обработку деталей сложной формы, высокоскоростную обработку, фрезерную обработку твердых материалов с высокой скоростью и точностью и многое другое. Эти машины нашли свое место в производстве различных приспособлений, пресс-форм, лопаток турбин, носовых обтекателей для реактивных двигателей, других изделий сложной форме и выполняют обработку с более высоким быстродействием по сравнению с обычным оборудованием.
Математическая модель гексапода включает в себя обратную и прямую кинематическую задачу. Решение обратной кинематической задачи для гексапода завязано на вычислении длины стоек и расположении шарниров при данном положении подвижной платформы. Разработка кинематической модели платформы в рассматриваемом случае имеет такие допущения:
- все шарниры считаются идеальными, в силу того что их оси строго перпендикулярны друг другу и пересекаются в одной точке;
- ось каждого линейного привода проходит через соответствующие центры шарниров;
- удлинение любой стойки можно определить без погрешностей;
- платформа собрана таким способом, что ориентация на ней шарниров точно известно. На (рис. 7) представлена конфигурация станка-гексапода с параллельной структурой. [5]
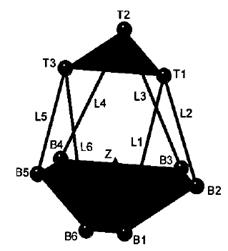
Рис. 7. Конфигурация станка-гексапода
Даны длины шести стоек L1, L2, L3, L4, L5, L6. Отношение положения начала верхней системы отсчета к началу нижней системы отсчета имеет вид [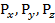 ]. Углы поворота (α, β, γ) определяются вращением верхней платформы: сначала на угол β относительно оси Y, далее на угол α относительно оси Х, и на угол γ относительно оси Z, в соответствии с (рис. 8).
]. Углы поворота (α, β, γ) определяются вращением верхней платформы: сначала на угол β относительно оси Y, далее на угол α относительно оси Х, и на угол γ относительно оси Z, в соответствии с (рис. 8).
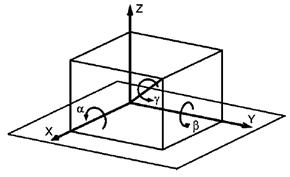
Рис. 8. Углы поворота
Соответственно выразим повороты вокруг осей X,Y,Z следующим образом:
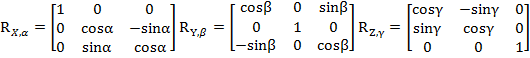 (1)
(1)
Запишем матрицу преобразования между подвижной верхней системой отсчета (ТОР) и неподвижной базовой системой отсчета (BASE) с помощью методов углов Эйлера:
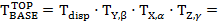
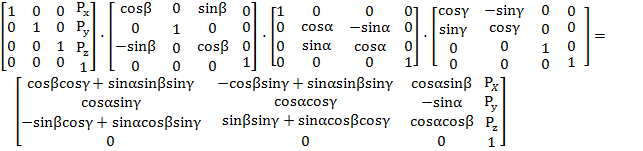 (2)
(2)
Приведем к базовой системе отсчета координаты вершин верхней системы отсчета, используя следующую матрицу преобразования:
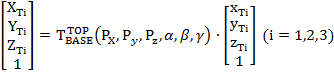 (3)
(3)
На (рис. 9) изображены геометрические размеры и конфигурация базовой и верхней платформы.
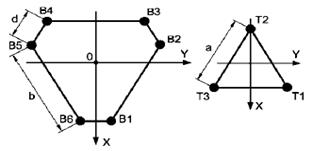
Рис. 9. Размеры верхней и базовой платформы.
Выразим в базовой системе отсчета координаты шести шарниров на базовой платформе согласно (рис. 9):
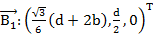
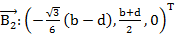
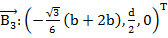
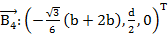 (4)
(4)
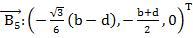
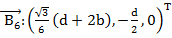
Запишем координаты трех шарниров на верхней платформе относительно базовой системы отсчета.
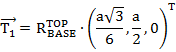
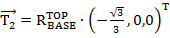 (5)
(5)
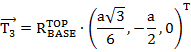
Следовательно, определим длины шести стоек: [5]
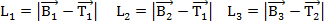 (6)
(6)
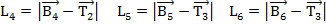
Для параллельного механизма построение прямой кинематической модели выполняется гораздо сложнее. Продемонстрируем построение прямой кинематической модели гексапода, пользуюсь (рис.7 и 9). В представленном варианте все кинематические преобразования находятся длинами 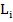 и положением стоек относительно к верхней платформе. На (рис.10) показаны геометрические характеристики трех спаренных треугольных структур (
и положением стоек относительно к верхней платформе. На (рис.10) показаны геометрические характеристики трех спаренных треугольных структур (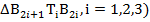 при известных длинах всех шести стоек.
при известных длинах всех шести стоек.
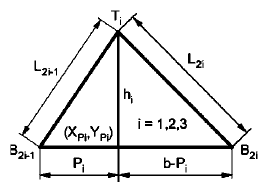
Рис. 10. Геометрические взаимосвязи спаренной структуры
Представим через вершины 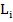 и
и 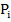 высоты трех спаренных треугольных структур (
высоты трех спаренных треугольных структур (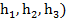 и запишем координаты
и запишем координаты 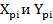 , где i=1,2,3 следующим образом:
, где i=1,2,3 следующим образом:
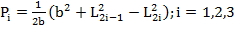
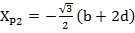
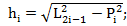 i=1,2,3
i=1,2,3 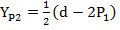 (7)
(7)
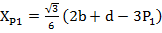
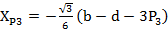
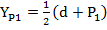
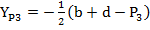
Ограничение на свободное перемещение накладывают три связанные между собой спаренные треугольные структуры (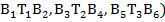 . Ели в качестве примера рассмотреть положение
. Ели в качестве примера рассмотреть положение 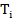 , то на него накладывается условие, что
, то на него накладывается условие, что 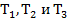 должны образовывать равносторонний треугольник с установленными размерами. Координаты вершин
должны образовывать равносторонний треугольник с установленными размерами. Координаты вершин 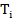 верхней платформы неизвестны, тогда координаты их проекций
верхней платформы неизвестны, тогда координаты их проекций 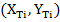 на плоскость X-Y будут находиться такими ограничениями:
на плоскость X-Y будут находиться такими ограничениями:
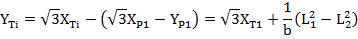
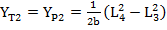 (8)
(8)
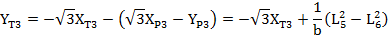
Найдем расстояние 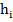 между вершиной
между вершиной 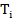 и точкой пересечения
и точкой пересечения 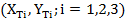 по формуле указанной ниже:
по формуле указанной ниже:
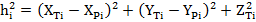 (9)
(9)
Чтобы замкнуть кинематическую цепь необходимо добавить еще три граничных условия, которые имеют вид:
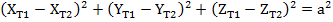
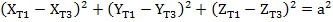 (10)
(10)
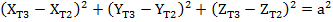
Комбинация выражений приведенных выше даст нам три нелинейных алгебраических уравнения с тремя переменными (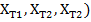 .
.
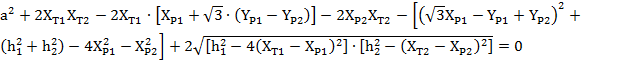 (11)
(11)
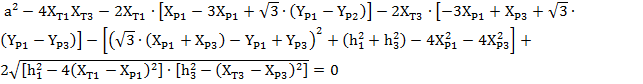 (12)
(12)
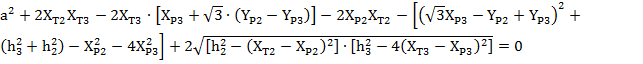 (13)
(13)
В силу того, что данные уравнения имеют высокую степень нелинейности, их точное решение сводится к невыполнимой задачи. Возможно лишь приближенное решение, которое имеет место быть лишь при помощи различных численных методов, таких как метод Ньютона Рафсона или оптимизационного алгоритма Левенберга-Маквардта, основанного на минимизации суммы квадратов невязок уравнений.
Так как координаты вершин верхней платформы определенны, то ее положение можно представить следующим образом:
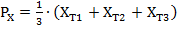
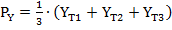 (14)
(14)
Для определения скоростей и ускорений рабочей платформы при движении по заданной траектории и сил, которые должны обеспечивать линейные приводы используется динамическая модель гексапода.
Из большого множества описанных динамический моделей самой удобной для описания динамики гексапода является модель Д'Аламбера. В его смысл заложен принцип, в котором говориться, что для получения уравновешенной системы сил, воздействующих на подвижную механическую систему, ко всем ее материальным точкам нужно, кроме фактически действующих на них активных сил и реакций связей, также условно приложить силы инерции точек. В данном случае подходят все уравнения статики для решения системы сил. Запишем математическую запись принципа следующим образом:
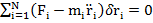 (15)
(15)
Где 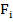 – сила, приложенная к материальной точке,
– сила, приложенная к материальной точке, 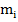 - масса материальной точки,
- масса материальной точки, 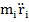 - сила инерции материальной точки,
- сила инерции материальной точки, 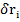 – смещение системы.
– смещение системы.
Вывод уравнений, описывающих динамику гексапода можно выполнить, опираясь на расчетную схему, которая изображена на (рис.11). На изображении представлено распределение масс, выраженное через центры тяжести различных компонентов. Где точка 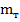 - центр тяжести верхней платформы, точка
- центр тяжести верхней платформы, точка 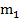 - центр тяжести цилиндра,
- центр тяжести цилиндра,  - центр тяжести поршня.
- центр тяжести поршня.
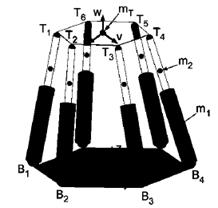
Рис. 11. Распределение масс гексапода
Рассматривая схему, упрощается вывод динамических уравнений за счет разделение всей системы на три подсистемы: поршни, цилиндры, платформа. Для определения результирующих сил, необходимых для каждой стойки, передвижения платформы приводятся к системе координат стоек.
На (рис.12) показаны силы, действующие на каждую стойку. Предполагается, что сила тяжести действует вертикально по нормали к плоскости основания.
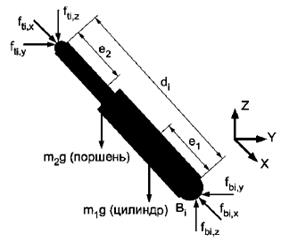
Рис. 12. Расчетная схема стойки
Рассматривается отдельно каждая стойка, как подсистема. При комбинации всех подсистем стоек формируется матричное уравнение, которое необходимо решить:
τ=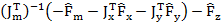 (16)
(16)
Где τ – вектор сил, действующих на стойки, 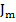 – матрица Якоби платформы,
– матрица Якоби платформы, 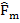 – суммарная сила, действующая на платформу,
– суммарная сила, действующая на платформу, 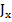 – матрица Якоби компонентов стоек гексапода по направлению оси Х,
– матрица Якоби компонентов стоек гексапода по направлению оси Х, 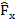 - суммарная сила, воздействующая на стойки в направлении оси X,
- суммарная сила, воздействующая на стойки в направлении оси X, 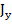 – матрица Якоби по направлению оси Y,
– матрица Якоби по направлению оси Y, 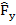 - суммарная сила по оси Y,
- суммарная сила по оси Y, 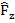 – суммарная сила в направлении оси Z.
– суммарная сила в направлении оси Z.
Решение уравнения даст неизвестные силы, действующие на каждую стойку.
Крайне не желательно, чтобы при работе гексапода подвижная платформа занимала сингулярные положения. Чтобы определить эти положения перед планированием траектории движения платформы, нужно вычислить определитель матрицы Якоби. Она дает связь между входными и выходными линейными скоростями стоек и угловыми скоростями подвижной платформы. Для гексапода (рис.11) входной вектор р, определяющий линейные скорости стоек представим в виде:
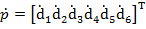 (17)
(17)
Запишем выходной вектор х, который определяет угловые и линейные скорости подвижной верхней опорой в виде:
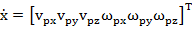 (18)
(18)
Так же запишем уравнение замкнутого контура для i-ой стойки в виде:
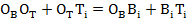 (19)
(19)
Где 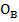 и
и 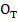 – центры верхней и базовой платформы
– центры верхней и базовой платформы
Продифференцируем уравнение (19) по времени и получим уравнение следующего вида:
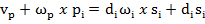 (20)
(20)
Где 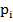 и
и 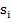 обозначают вектор
обозначают вектор 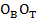 и единичный вектор, направленный вдоль
и единичный вектор, направленный вдоль 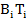 ;
;
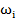 – угловая скорость i-ой стойки относительно базовой системы отсчета в точке
– угловая скорость i-ой стойки относительно базовой системы отсчета в точке 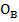 , рад/с;
, рад/с;
Скалярно умножим обе части уравнения (20) на 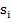 , то
, то 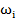 сократиться и уравнение примет следующий вид:
сократиться и уравнение примет следующий вид:
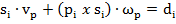 (21)
(21)
Комбинирование шести полученных скалярных уравнений для каждой стойки и уравнение (21) дадут матричное уравнение:
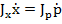 (22)
(22)
Соответственно когда определитель матрицы 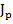 равен нулю она определяет первый тип сингулярности (с потерей степеней свободы), аналогично если определитель матрицы
равен нулю она определяет первый тип сингулярности (с потерей степеней свободы), аналогично если определитель матрицы 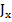 равен нулю, то это второй тип сингулярности (с добавлением степеней свободы). [5]
равен нулю, то это второй тип сингулярности (с добавлением степеней свободы). [5]
Выразим матрицу 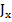 в виде:
в виде:
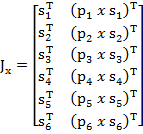 (23)
(23)
Так как матрица 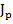 единичная, то это значит, что в гексаподе будет отсутствовать первый тип сингулярности, а именно все сингулярности в гексаподе будут связаны с появлением дополнительных степеней свободы платформы.
единичная, то это значит, что в гексаподе будет отсутствовать первый тип сингулярности, а именно все сингулярности в гексаподе будут связаны с появлением дополнительных степеней свободы платформы.
Особого внимания заслуживает вопрос, связанный с анализом состояния машиностроительного производства. В его развитии можно выделить две эры – индустриальную и информационную. Первая эра брала свои истоки с прошлого века, характеризующаяся преимущественным развитием отраслей материального производства и в первую очередь промышленности. [2] Производство становится массовым, крупносерийным с ориентацией на объемные рынки и на изделия большого спроса. Индустриальная эра сменяется информационной, переход которой в ведущих странах Запада начался в 60 годы. Основным отличием данной эры является преимущественный рост экономики сферы услуг (в валовом продукте), а главным образом отраслей, которые связаны с переработкой информации и осуществлением посреднической деятельности всех видов. Производство становится в высшей степени гибким с ориентацией на индивидуальные запросы потребителей, не массовым и на небольшие по объему рынки сбыта. Наблюдается изменение труда, так как в индустриальную эру он состоял преимущественно из физического труда производственных рабочих, что нельзя сказать про информационную эру, в которой основу составлял инженерный и управленческий труд. [2] Ушли, времена, когда жизненный цикл продукции мог длиться десятилетиями. В современное время в машиностроении он сокращен до 3-5 лет и по истечению этого времени необходим полная смена средств технологического обеспечения и замена выпускаемых изделий. Таким образом, заметна тенденция сокращения жизненного цикла изделия, которая выражена стремлением производителей плотно и быстрее удовлетворить потребности общества. Растет потребность общества, которое порождает рост машиностроительных изделий.
К основным недостаткам машиностроительного производства можно отнести избыточное разнообразие выпускаемых изделий и средств технического обеспечения, неприспособленность производства к быстрой эффективной перестройке на выпуск новой продукции. Так же оказывает влияние на избыточное разнообразие изделий низкий уровень унификации, как самих изделий, так и их деталей. Низкий уровень типизации номенклатуры изготовляемых деталей порождает излишнее разнообразие технологических процессов, которое влечет за собой рост разнообразия технологических средств.
В результате большинство инженерно-технических работников ежегодно выполняют одни и те же работы, одни и те же задачи, что влечет огромные расходы труда, времени и материальных средств. Идет множество решений, повторяющих или улучшающих уже известные. В итоге наблюдается распыление сил, бесконечное дублирование работ, что влечет за собой создание необоснованно большого разнообразия средств технического обеспечения, существенная часть которых оказывается нестандартизованной. [2]
Можно сделать вывод, что машиностроительное производство характеризуется изготовлением большого числа одних и тех же или близких друг другу деталей, сборочных единиц; значительным дублированием технологической подготовки производства; огромным разнообразием технологических процессов, оборудования оснастки; большим объемом ежегодного обновления физически неизношенных технологических средств; невысокой гибкостью производства.
В связи с анализом актуально будет представить пути совершенствования машиностроительного производства, которые направлены на сведение к минимуму разнообразия технологических процессов, оборудования, оснастки, невостребованности технологического оборудования, повышение гибкости и мобильности производства и т.д.
Первый путь перестройки машиностроительного производства базируется на системе взаимосвязанных классификаций изделий и средств технологического обеспечения. Классификации оказывают существенное влияние на эффективность развития любой человеческой деятельности. От того как правильно разработана классификация, зависит конечный результат.
Еще одним не мене важным мероприятием является широкая типизация и унификация, как самих изделий, так и средств технологического обеспечения.
Рассмотрим модуль поверхностей детали, как один из основных путей совершенствования машиностроительного производства. «Модульный принцип – особенность построения технических систем, заключающаяся в подчинении их размеров проектному модулю (модулям) и (или) в обеспечении возможности комплектования различных сложных нестандартных технических систем с большим различием характеристик из небольшого, экономически обоснованного количества типов и типоразмеров одинаковых первичных общих модулей-элементов»[4]. Организация подготовки производства с использованием модульного принципа позволит осуществить скачек в повышении эффективности машиностроения, с минимальными расходами.
Выводы.
Таким образом, в работе был представлен обзор существующих и работающих в машиностроительном производстве станков с параллельной кинематикой. Выявлены их классификация и конструктивные особенности. В результате анализа были определены достоинства и недостатки параллельных установок, и их приоритет перед станками с прямоугольной системой координат. Так же основным достоинством параллельной кинематики является более высокие динамические характеристики.
В данной статье предложен простой в вычислительном отношении алгоритм решения задач динамики параллельных механизмов, основанный на модели Д'Аламбера. Рассмотрены обратная и прямая задачи кинематики на базе гексапода. Найдены мероприятия на пути совершенствования машиностроительного производства, основой которого является модульный принцип, который позволяет повысить технико-экономические показатели, расширить технологические возможности станков с параллельной кинематикой, сократить затраты по внедрению станков нового поколения.
Библиографическая ссылка
Зеленков Д.А., Астапов В.Н. НОВЫЕ ТЕХНОЛОГИИ МЕХАНИЧЕСКОЙ ОБРАБОТКИ НА СТАНКАХ С ПАРАЛЛЕЛЬНОЙ КИНЕМАТИКОЙ // Международный студенческий научный вестник. – 2018. – № 6. ;URL: https://eduherald.ru/ru/article/view?id=19350 (дата обращения: 20.04.2024).