Понятие развивающихся систем приобретает все большее значение в различных отраслях науки. На сегодняшний день важными примерами этих систем могут служить различные отрасли экономики; отдельные предприятия, производственно-технические объединения; вычислительные центры и научно-технический прогресс в целом.
Как искусственные, так и природные системы должны иметь вначале развития наличие определенных первоначальных ресурсов, таких как энергия, информация и вещество. Должен учитываться характер условий внешней среды, при взаимодействии с которой создает потребляемый продукт. Должны выполняться некоторые балансовые соотношения между элементами объединений, поступающими в динамическую систему, и продуктами динамической системы. Такая связь должна быть функциональна и иметь взаимозависимость между ресурсами, затрачиваемыми на внутреннее развитие и на выполнение внешних функций динамической системы и результатами функционирования системы. Помимо этого необходимо учитывать конкурентное поведение, износ технологий и трудовые ресурсы.
Динамическая система в экономике рассматривает с точки зрения математической модели, с множеством символических математических объектов и отношений между ними. Математическая модель будет воспроизводить выбранные стороны развивающейся системы, если будут установлены правила соответствия, связывающие специфические объекты и отношения системы с определенными математическими объектами и отношениями.
Известны различные детальные и обобщенные классификации моделей экономических систем, в той или иной мере удовлетворяющие практическим целям. Для удобства экономические модели делятся: на макромодели экономического роста с детальным описанием производственно-технологических возможностей и их изменением во времени; на микромодели равновесия с описанием непроизводственной сферы и описанием механизмов, регулирующих обмены и распределение производственной продукции; макромодели равновесия рассматривают хозяйство в целом; модели глобальной динамики, изображая процесс расширения производства и взаимодействия с процессами в непроизводственной сфере.
В статье рассматривается классическая модель типа «затраты – выпуск», где уровень выпуска каждого продукта пропорционален его суммарным затратам во всех других отраслях. Пусть предприятие предоставляет два [к примеру] вида услуг: P1 (массовая обработка ) и дополнительно P2 (спец. заказы), при наличии двух дефицитных ресурсов S1 и S2. Под S1 понимаются затраты электроэнергии для работы оборудования и созданий условий работы, а под S2 – трудовые ресурсы. При подсчете рентабельности учитывается чистая прибыль предприятия. Ниже приведены данные необходимые для решения поставленной задачи (в расчет на 1000 изготовленных единиц)[4-7]
|
Ресурсы |
S1 |
S2 |
Удельные затраты на оказание услуг (млн. руб.) |
Прибыль (млн. руб.) |
|
Обработка |
Нормы расхода ресурсов (тыс. руб.) |
|||
|
P1 |
780 |
250 |
0.009 |
0.045 |
|
P2 |
560 |
195 |
0.007 |
0.078 |
|
Запасы ресурсов (тыс. руб.) |
950 |
600 |
Условно-постоянные затраты (млн. руб.) |
|
Пусть x1 и x2 это объем оказания услуг, тогда чистая прибыль составит
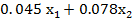млн. руб.,
а затраты будут равны
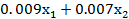млн. руб.
Рентабельность вычисляется по формуле:
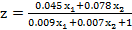(1)
Ограничения по затратам электроэнергии и трудовых ресурсов записывается в виде неравенств:
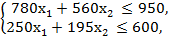(2)
Учитывая неотрицательность переменных x1 и x2 , а также (1) и (2), получается задача дробно-линейного программирования:
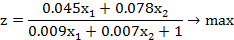
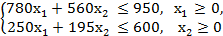(3)
Необходимо эту задачу свести к задаче линейного программирования. Знаменатель функции цели обозначается через 
:
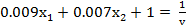(4)
Так как v≠0, то имеет смысл умножить на него обе части каждого неравенства в системе ограничений, прим это смысл неравенств сохраняется. Уравнение (4) подвергается такому же преобразованию. Система ограничений записывается в виде:
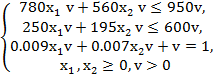(5)
С учетом (4) преобразуется функция цели:
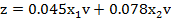
Вводятся новые переменные y1=x1z; y2=x2v (6)
Окончательная задача запишется в виде:
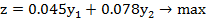
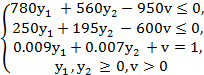
Это задача линейного программирования. Для ее решения необходимо исключить v из первых двух ограничений. Для этого третье ограничение, умноженное на 950 прибавляется к первому, затем третье ограничение, умноженное на 600 прибавляется ко второму. Система примет вид:
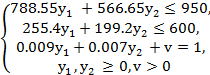
Необходимо выразить v из последнего уравнения:
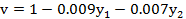(7)
Положительное v необходимо отбросить, так как баланс нарушился, то уравнение заменится неравенством. В результате проведенных преобразований получается задача линейного программирования, содержащая всего две переменные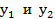 
.
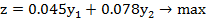
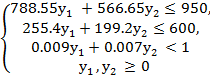
Эту вспомогательную задачу возможно решить графически.
Для построения прямых используются следующие пары точек, например:
(l1) 788.55y1 + 566.65y2 =950 A1 (0;1.68)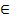
l1, A2 (1.2;0) 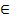l1,
(l2) 255.4y1 + 199.2y2 =600 B1 (0; 3.01)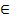 l2, B2(2.35 ;0) 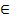l2
(l3) 0.009y1 + 0.007y2 =1 C1 (0; 142.9) 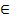l3, C2 (111.1 ;0)
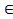l3
Система координат с областью допустимых решений и вектором целевой функции приведена на рис.1.
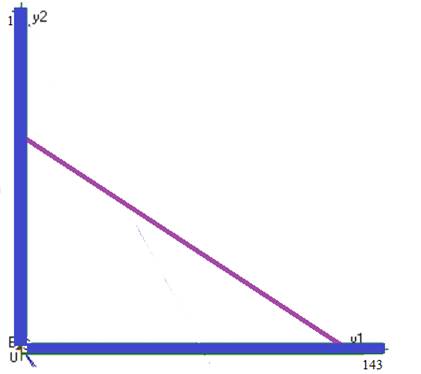
Рис.1
Построим вектор целевой функции z (0.045;0.078)
Как видно из графика, максимальной вершиной области допустимых значений будет вершина (1,20474288;0)
В данной вершине значение целевой функции равно:
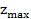= 0.045 * 1,20474288 + 0.078 *0
И в результате :
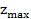=0,05421343
Вывод: Рентабельность составляет 5%
Рассмотрим второй способ решения [8,9]:
Необходимо решить систему уравнений
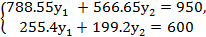
В результате получаются значения переменных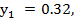 
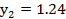
Yопт=(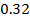
;
)
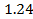Подставим получившиеся значения в целевую функцию:
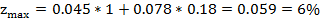
Вспомогательная задача решена. Необходимо определить значение v по формуле (7) для вычисления xопт.
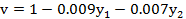
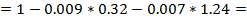0.98
Далее необходимо найти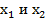 
:
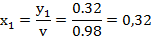
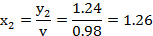
xопт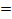
(0.32;1.26),
Вывод: При количестве 32 массовых заказов и объеме изготовления 126 индивидуальных запросов, рентабельность составит 6%
Библиографическая ссылка
Алашеева Е.А., Рогова Н.В., Шевелева К.И. ПОВЫШЕНИЕ РЕНТАБИЛЬНОСТИ НА ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЯХ // Международный студенческий научный вестник. – 2018. – № 6. ;URL: https://eduherald.ru/ru/article/view?id=19276 (дата обращения: 16.04.2024).