Метод оценки качества транспортного обслуживания включает в себя несколько основных аспектов (1), необходимых для оценки качества: время, затраченное на поездку, фактически затраченное время, наполнение транспорта (коэффициент) и регулярность движения [1]:
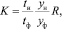
где tн – норматив времени, затраченный пассажиром на поездку (40 мин. для городов с числом жителей более 1 млн., 35 мин. – от 500 тыс. до 1 млн, 30 мин. – от 250 тыс. до 500 тыс., 25 мин. – менее 250 тыс.); tф – время, фактически затраченное пассажиром на поездку; yн – нормативный коэффициент наполнения транспорта (считается, что в среднем не более 0.3, а в часы пик около 0.8); yф – фактическое значение коэффициента наполнения; R – показатель регулярности движения;
,
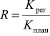где Kрег – коэффициент регулярности на маршруте; Kплан – план регулярности на маршруте.
,
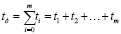В данном случает tm время в текущий момент (сумма времени (массив) по всей длине пути, будет являться фактическим временем, затраченным на проезд от начала пути до точки назначения).
Нормативный коэффициент наполнения транспорта принимается в среднем 0,5 условных единиц, а фактический рассчитывается из отношения количества пассажиров ко времени проезда от заданной точки до конечного пути, а также отношения свободных и занятых мест [2].
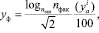
где i=0 до nфак–1;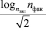 
– логарифмическое отношение максимальной загруженности (nзап) к фактической загруженности (nфак) пассажиров; 
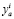– текущее значение коэффициента наполненности автотранспорта.
Коэффициент регулярности на маршруте, это показатель частоты проезда автобусов заданной точки за определенное время.
,
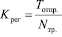где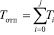 
,
где j – количество отправлений; Nтр – количество транспорта за определенное время (как правило берется график отправлений транспорта за промежуток времени).
Составим имитационную модель движения пассажирского автотранспорта и использованием AnyLogic 6.
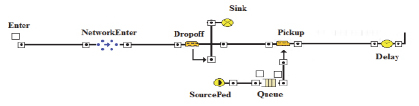
Рис. 1. Имитационная модель движения автотранспорта (автобуса)
Переменные среды и функции, используемые в работе:
Network – объект задания топологии маршрутной транспортной сети.
Source – генератор автобусов. Автобусы выходят на линии в соответствии с действующим расписанием. В данном случае будем использовать модуль расписаний Schedule.
NetworkEnter – объект задает вход в транспортную сеть. Отображение объектов в момент входа в транспортную сеть.
NetworkMoveTo – объект моделирует перегон маршрута. Данный объект указывает транспортному средству путь следования к ближайшему остановочному пункту.
SourcePed – генератор пассажиров на остановочном пункте. У каждого пешехода есть определенные характеристики: место назначения, наличие проездного билета. Данная модель может быть дополнено любым типом пассажиров.
Queue – модель очереди ожидающих посадки пассажиров.
Pickup – вместе с объектом Dropoff моделирует посадку-высадку пассажиров.
Delay – объект моделирует время простоя автобуса на остановочном пункте.
Цикл продолжается до тех пор, пока моделируется объект Delay.
Конечно, при построении модели (рис. 1) использовались некоторые допущения, например время рассинхронизации движения автобуса (отклонение от расписания) минимально, величина пассажиропотока постоянна.
Для использования уравнения оценки качества обслуживания городского транспорта, в имитационной модели были заложены только базовые показатели. Логическая схема основанная на нечеткой логике, построенная на основе имитационной модели приведена на рис. 2.
Для использования уравнения оценки качества обслуживания городского транспорта, в имитационной модели были заложены только базовые показатели:
– время поездки транспортного средства (счетчик стартует при прохождении отрезка NetworkEnter, причем сравнивая исходное время, затраченное автобусом с учетом минимальной остановке на каждом узле загрузки/выгрузки пассажиров, t1 и t0 – текущее время проезда и номинальное время соответственно). В данном случае полное время прохождения маршрута было принято взять 20 минут (1200 с), считать для маленького города;
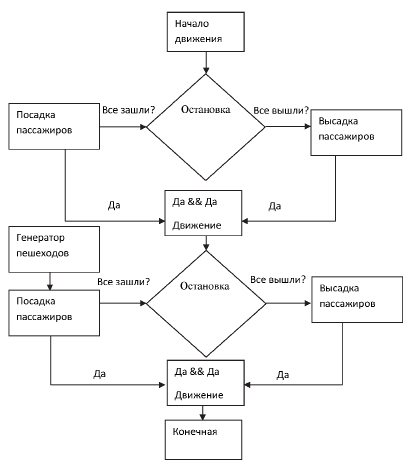
Рис. 2. Движение автобуса, описанное с помощью нечеткой логики
– коэффициент наполнения автобуса, функция Dropoff, которая отвечает не только за остановки и загрузку/выгрузку пассажиров, но и за коэффициент отношения наполненности транспорта (номинальный к фактическому). Номинальный коэффициент наполненности автобуса примем 0,5;
– показатель регулярности движения. С какой периодичностью ходят автобусы за время прохождения фактического маршрута. Автобусы ходят каждые 10 минут (задано по умолчанию). Максимальная загруженность автобуса 100 человек (номинальная 50 человек).
На основе имитационной модели составим математическую модель.
.
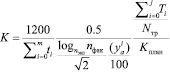Математическая модель оценки качества обслуживания пассажирского транспорта.
Алгоритм оценки качества обслуживания пассажирского транспорта [3]:
– определить коэффициент регулярность автотранспорта (время пути транспорта по заданному маршруту);
– определить фактический коэффициент наполнения автотранспорта (среднее количество пассажиров данного вида автотранспорта за заданный период времени);
– определить показатель регулярности движения (как часто осуществляется отправление пассажирского транспорта).
Библиографическая ссылка
Иванов В.С., Рыбанов А.А., Короткова Н.Н. ИССЛЕДОВАНИЕ МЕТОДОВ И ПРОГРАММНАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА ОЦЕНКИ КАЧЕСТВА ОБСЛУЖИВАНИЯ ПАССАЖИРОВ ГОРОДСКОГО ТРАНСПОРТА // Международный студенческий научный вестник. – 2018. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=18382 (дата обращения: 21.11.2024).