При проведении решения многих проблем, которые возникают в радиотехнике, электро- и радиосвязи, радиофизике и других научно-технических отраслях, требуется обладать информацией о том, какая структура электромагнитных полей в рассматриваемых частях пространств.
Среди таких проблем можно выделить, например, разработку излучающих систем (в антенных структурах) и увеличение их помехозащищенности, создание электромагнит-ной совместимости в радиотехнических устройствах и системах, проведение разработки разных линий передачи энергии и различные другие. При расчете электромагнитных полей в каждых конкретных случаях необходимо решать соответствующие электродинамические задачи.
Учеными выделяются два вида задач электродинамики, их называют прямыми и обратными задачами.
В прямых электродинамических задачах (их могут называть еще и задачами, направленными на анализ) заключаются в том, что определяется электромагнитное поле, которое формируется в рассматриваемых частях пространств при воздействии известных (заданных) источников.
В обратных электродинамических задачах (во многих случаях их рассматривают как задачи синтеза) состоят при определении системы источников, которые формируют электромагнитные поля, обладающие необходимой (заданной) структурой.
Появляющиеся в практической деятельности электродинамические задачи во многих случаях довольно сложны, и получать их решения удается только после того, как введен ряд упрощающих предположений. В этой связи на практике всегда вместо реальных задач рассматривают определенную модельную задачу, в которой в какой-то мере идет отражение реальной ситуации.
Во многих случаях исходные задачи удается разбить на совокупность более простых, в каждой из которых можно учитывать один или несколько тех факторов, которые влияют.
Наиболее известной и широко изученной обратной задачей является задача, связанная с определением характеристик объектов по их электромагнитным излу чениям, говорят о так называемой пассивной локации.
Не менее распространенными являются задачи в которых необходимо проводить восстановление параметров объектов по отраженным излучениям – задачи, связанные с активной локацией.
Указанный класс задач тоже представляет заметный интерес и его изучили достаточно хорошо.
В простейших случаях, под локацией понимают задачи, связанные с нахождением расстояний до источников и направлений от него до наблюдателей. Для более сложных случаев, задача локации заключается в том, что определяется форма источника и определяются его электрофизические свойства.
В предлагаемой вниманию статье мы анализируем методику, связанную с тем, что проводится оценка макропараметров, относящихся к поглощающим компонентам. Такие компоненты располагают на поверхности тел, со сложной формой.
Определение значений макропараметров происходит основываясь на том, что известны данные по измерений рассеивающих характеристик тел по заданным углам наблюдения.
Значения исследуемых измеряемых величин определяется, (если не принимать во внимание ошибки, связанные с измерениями) большей частью тем, какие рассматриваются условия наблюдения (частотные, поляризационные особенности, описывающие процесс передачи информации, распространения радиоволн), при этом еще необходимо понимать, какими топологическими и радиофизическими свойствами описываются анализируемые объекты [1, 2].
Для измеренных величин S (мы можем, например, проводить анализ зафиксированных значений электромагнитных полей, которые меняются по углу наблюдения) на базе формального подхода есть возможности представления их как результат вывода какого-либо оператора S: S{Y,W[F,R(G,P)]}, в приведенной формуле Y – дает описание совокупности значений по тензору анализируемых условий, T – позволяет описать характеристики, связанные отражениями от тел радиоволн, они основываются на геометрических формах F, а также макропараметрах, описывающих поглощающие компоненты, размещаемых на поверхностях тел.
Существует связь макропараметров, относящихся к поглощающим компонентам и координат, описывающих их расположение на поверхностях тел, а также магнито-диэлектрических характеристик веществ [3, 4].
Нам необходимо осуществить процесс решения обратной задачи, что связано с оценкой элементов в конечном множестве P, причем мы используем информацию об S. Важно построить алгоритм, который позволит провести минимизацию функции невязки A, она показывает зависимость между математической моделью в расчетах S и измеренной характеристикой S0:
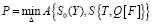 , (1)
, (1)
В приведенном выражении D представляет собой пространство, содержащее возможные значения элементов, которые есть в множестве P.
С тем, чтобы дать описание оператора S в (1), требуется привлекать математическую модель, позволяющую провести описание процесса, связанного с рассеянием радиоволн на телах со сложной формой. Нами для расчета характеристик рассеянных радиоволн был рассмотрен метод интегральных уравнений.
Для функции невязки использовалось такое представление:
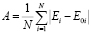 , (2)
, (2)
В нем E0i – представляет собой определенное (полученное в результате измерений) значение для величины электромагнитного поля анализируемого тела (S0), Ei – представляет собой теоретическую оценку (вследствие применения оператора S).
Когда решается задача, связанная с тем, что минимизируется A важно использовать методики, относящиеся к нелинейному программированию, вследствие того, что создаваемая функция будет иметь много экстремумов. С тем, чтобы осуществить решение такой задачи, был применен метод сеток [5], в нем последовательным образом уменьшалась область определяемых значений.
Во внутренней области каждого из участков на сетке применялся метод, позволяющий провести локальную оптимизацию – метод хорд [5].
Когда проводилась оценка возможностей созданной методики, нами была рассмотрена модельная задача, в ней определялись параметры поглощающей компоненты, ее мы рассматривали в виде однородного магнитодиэлектрического слоя, характеризующегося толщиной g (рис. 1).
В результате проведения машинного эксперимента, на базе метода интегральных уравнений осуществлялся расчет диаграмм обратного рассеяния (ДОР) анализируемых тел.
Поля, рассеянные телами со сложной формой, определялись исходя из приближения Стрэттона-Чу [6–8]:
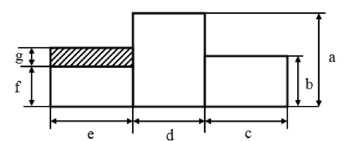
Рис. 1. Схема рассеяния радиоволн на объекте сложной формы с поглощающей компонентой
Когда рассматривалась поглощающая компонента, то мы исходили из того, что она описывается на основе комплексной диэлектрической проницаемости 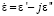 , а также действительной неотрицательной магнитной проницаемости m.
, а также действительной неотрицательной магнитной проницаемости m.
Мы исходили из того, что значения, относящиеся к магнитной и диэлектрической проницаемости лежат во внутренней области интервала 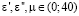 .
.
Мы можем считать, что это хорошо согласуется с анализом относительно разных видов радиопоглощающих материалов, которые приводятся в различных источниках. Процесс моделирования проводился для длины волны, которая была равна l=0,05 м.
В процессе решения задачи, нами проводился выбор некоторого значения m, которое лежит в указанном интервале и осуществлялось решение задачи оптимизации, которая основывалась на определении значений 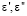 . После определения значений
. После определения значений 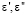 , требуется проводить решение одномерной задачи оптимизации, в ней определялось значение m, которое относится к внутренней области указанного интервала.
, требуется проводить решение одномерной задачи оптимизации, в ней определялось значение m, которое относится к внутренней области указанного интервала.
При расчете Q, важно осуществить суммирование по индексу i для таких углов, которые описывают значения локальные максимумы для тех углов, которые θ∈[0°,θmax]. Мы рассмотрели значение θmax=28°, исходя из того, что указанный угол относится к области, связанной с зеркальным отражением..
Процесс моделирования проводился для резонансных размеров тел:
1λ<a,b,c,d,e,f<9λ, g=0,05l.
Основываясь на рассматриваемом подходе, мы провели расчеты оценок относительно характеристик поглощающих компонентов.
Мы показали, что если размеры сетки равны 115×115, тогда когда рассматривается сформулированная двумерная оптимизационная задача значения ε′ и ε′′, по 1 шагу, определены с ошибкой, не превышающей 42 %. Значения ε′ и ε′′, найденные на 2 шаге (когда сужается вдвое область, внутри которой лежат возможные значения ε′ и ε′′) описывались ошибкой, не превышающей 7 %.
На рис. 2 приведены графические зависимости, показывающие поведение ДОР используемой нами модели [9, 10], в которую могла входить поглощающая компонента.
Была также рассмотрена задача, для модельных компонент, в которых комплексная магнитная проницаемость 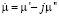 и действительная диэлектрическая проницаемость ε>0. Мы исходили из того, что значения указанных параметров относятся к внутренней области интервала
и действительная диэлектрическая проницаемость ε>0. Мы исходили из того, что значения указанных параметров относятся к внутренней области интервала  . Проводился анализ для длины волны, которая была равна λ=λ0=0.05 м.
. Проводился анализ для длины волны, которая была равна λ=λ0=0.05 м.
Процесс определения 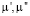 , а также e проходил таким же образом, как это было указано выше – вначале решалась двумерная задача оптимизации, а затем – одномерная.
, а также e проходил таким же образом, как это было указано выше – вначале решалась двумерная задача оптимизации, а затем – одномерная.
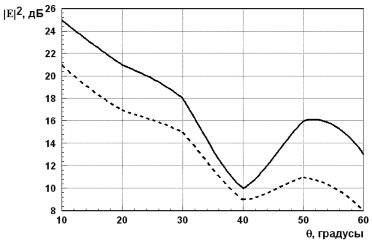
Рис. 2. Диаграмма обратного рассеяния объекта: 1 – без поглощающей компоненты, 2 – с поглощающей компонентой
Мы показали, что если размеры сетки будут 115×115, то при решении сформулированной двумерной оптимизационной задачи те значения 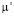 и
и 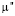 , которые были найдены для 1 шага, имеют ошибкой, не превышающую 41 %. Те значения
, которые были найдены для 1 шага, имеют ошибкой, не превышающую 41 %. Те значения 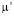 и
и 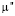 , которые были найдены на 2 шаге, имели ошибку не превышающую 7 %.
, которые были найдены на 2 шаге, имели ошибку не превышающую 7 %.
В результате, проанализированный подход, в котором решалась обратная задачи дифракции на основе метода интегральных уравнений, а также алгоритмов, которые позволяли решать многоэкстремальные оптимизационные задачи, позволяет рассчитать оценки параметров поглощающих компонент, которые размещены на поверхностях тел со сложной формой.
При этом в качестве исходных данных используются экспериментальные данные для угловых зависимостей ДОР.
Вследствие применения нескольких поглощающих компонент, которые имеют определенные параметры, есть возможности для обеспечения необходимых уровней рассеянных электромагнитных полей.
Библиографическая ссылка
Казаков Е.Н. ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЭЛЕКТРОДИНАМИЧЕСКИХ МАТЕРИАЛОВ // Международный студенческий научный вестник. – 2018. – № 3-3. ;URL: https://eduherald.ru/ru/article/view?id=18300 (дата обращения: 26.04.2024).

