Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ширяева М.С. 1

---

1 ФГБОУ ВО «Ставропольский государственный аграрный университет»

Актуальность темы обусловлена тем, что использование методов оптимизации позволяет с максимальной выгодой и минимальными расходами решить задачу о производстве определенной продукции, найти более выгодный вариант и составить наиболее оптимальный план, а также сбалансированный режим работы. Решение оптимизационной производственной задачи играет важную роль в развитии производства в целом. В процессе построения математической модели для решения определяются величины, с помощью которых должна быть построена модель. На переменные накладываются ограничения при которых выполняются условия, характерные для моделируемой системы. Определяется цель задачи, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи. Для построения модели идентифицируются переменные, а цель и ограничения представляется в виде математических функций этих переменных. Надлежащий анализ вопросов подобного рода и корректная формулировка математической модели являются центральным звеном решения задач линейной оптимизации.

Статья в формате PDF

0 KB

линейная оптимизация

принятие решений

симплекс – метод

математическая модель

1. Долгополова А.Ф. Моделирование стратегии управления в социально-экономических системах с использованием Марковских процессов // Вестник АПК Ставрополья. – 2011. – № 1 (1). – С. 67–69.

2. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Особенности применения методов математического моделирования в экономических исследованиях // Kant: Экономика и управление. – 2013. – № 1. – С. 62–66.

3. Линейная алгебра / Крон Р.В., Попова С.В., Смирнова Н.Б., Долгих Е.В. // учебное пособие для студентов вузов сельскохозяйственных, инженерно-технических и экономических направлений. – М., 2015.

4. Логинова Я.А., Долгополова А.Ф. Использование элементов линейной алгебры в экономических расчётах // Международный студенческий научный вестник. – 2016. – № 3–3. – С. 393–395.

5. Манько А.И., Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Обзор методов социально-экономического прогнозирования и их применение в реальной экономике // Наука и образование: современные тренды. – 2015. – № 2 (8). – С. 438–448.

6. Немцова А.В., Попова С.В. Применение средств матричной алгебры для решения задач экономического содержания // Современные наукоемкие технологии. – 2014. – № 5–2. – С. 171 – 172.

7. Цысь Ю.В., Долгополова А.Ф. Элементы линейной алгебры и их применение при решении экономических задач // Современные наукоемкие технологии. – 2013. – № 6. – С. 91–93.

Актуальность выбранной темы обусловлена тем, что использование методов оптимизации, в том числе и линейного программирования, позволяет с максимальной выгодой и минимальными расходами решить задачу о производстве определенной продукции, найти более выгодный вариант, составить наиболее оптимальный план, а также сбалансированный режим работы. Решение оптимизационной производственной задачи играет важную роль в развитии производства в целом и обосновании эффективности производственных процессов [2].

В управлении производством методы оптимизации влияют на нахождение наилучших хозяйственных решений, которые могут обеспечивать максимальное значение целевой функции и минимальное значение затрат. Необходимость поиска подобного рода решений объясняется наличием различных ограничений на факторы производства, позволяющие предприятиям полноценно и бесперебойно функционировать. Отсутствие подобных ограничений привело бы к недостаточному количеству вариантов решений [1].

Качество решения большинства экономических задач зависит от наиболее эффективного способа использования ресурсов (сырья, денег, оборудования). Именно эффективностью использования ограниченных ресурсов определяется конечный результат деятельности предприятия [4].

Экономическая суть методов оптимизации заключается в том, что, выбирается такой способ распределения ресурсов предприятия, при котором обеспечивается максимум (или минимум) интересующего ЛПР показателя.

Задачи нахождения значений параметров, обеспечивающих экстремум функции 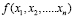при наличии ограничений, наложенных на аргументы 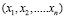, носят общее название – задач математического программирования [5].

Среди задач математического программирования самыми простыми и наиболее хорошо изученными являются так называемые задачи линейной оптимизации. Для них характерно то, что целевая функция линейно зависит от 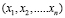, а также то, что ограничения, накладываемые на независимые переменные, имеют вид линейных равенств или неравенств относительно этих переменных [7].

Такие задачи часто встречаются на практике при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта. Во многих случаях расходы и доходы линейно зависят от количества закупленных или утилизированных средств.

Как уже отмечалось, оптимизация, включающая теорию и методы решения задач, в которых критерий оптимальности (целевая функция) линейно зависит от параметров задачи, является наиболее разработанным разделом информационных технологий оптимальных решений. Линейные модели широко используются в теории и практике принятия управленческих решений.

Общая задача линейной оптимизации заключается в нахождении максимума (минимума) линейной целевой функции. Функция f(x) называется целевой функцией, критерием оптимальности или линейной формой.

Вектор значений неизвестных 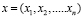, удовлетворяющих условию задачи, называется допустимым решением или допустимым планом задачи линейной оптимизации. Совокупность всех допустимых планов называется множеством допустимых планов. Допустимое решение называется оптимальным, если оно обеспечивает максимальное (или, в зависимости от условий задачи, – минимальное) значение целевой функции.

Решение задач линейной оптимизации может быть получено без особых затруднений. Классическим методом решения задач данного типа является симплекс-метод. В случае лишь двух переменных успешно может использоваться также графический метод решения, обладающий преимуществом наглядности [6].

Рассмотрим пример решения задачи на нахождение оптимальных значений функции.

Для производства однородной продукции используется три вида сырья – сталь, железо, медь и две технологии – выплавка и ковка. Производительность первой технологии (выплавки) составляет 20 ед. продукции в час, производительность второй технологии (ковки) составляет 30 ед. продукции в час. Необходимое количество сырья (в кг) каждого вида, которое расходуется за 1 час при использовании первой и второй технологий и общие запасы сырья – стали, меди и железа имеющиеся на складе, приведены в таблице.

Определить план производства с использованием первой и второй технологий, при которых выпуск будет максимальным.

Пусть x1 и x2 – время использования первой и второй технологий соответственно. Тогда объем выпуска продукции с учетом производительности технологий равен:

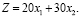
Учитывая ограничения на запасы сырья, получаем следующие неравенства:

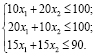
В результате имеем задачу:

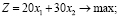
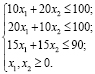
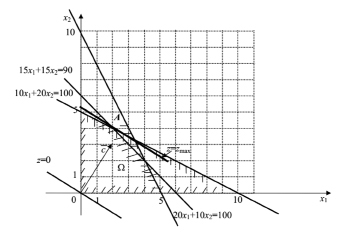
Построим область допустимых решений (рисунок).

Так как, данная задача является задачей на максимум, то прямую 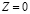нужно перемещать в направлении вектора 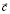. В результате опорная прямая проходит через точку А и координаты этой точки можно получить, как точку пересечения прямых линий на плоскости [3]:

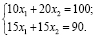
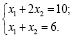
Получаем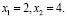

Значение целевой функции в оптимальной точке

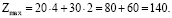
В результате расчетов можно сделать вывод о том, что максимальный объем продукции будет получен в результате использовании первой технологии в течении 2 часов и второй технологии в течение 4 часов их работы.

Таким образом, в результате проведенного исследования можно сделать вывод о том, что применение методов оптимизации приводит к рациональному использованию ресурсов и, следовательно, к более эффективному функционированию предприятия.

Библиографическая ссылка