Параллельное программирование появилось уже более 50 лет назад, тогда, когда были изобретены каналы – независимые аппаратные контроллеры, позволяющие в центральном процессоре исполнять прикладные программы одновременным образом с разными операциями, связанными с вводом-выводом других программ. Сначала работы по параллельному программированию в основном были в области операционных систем. К концу 1960-х годов были сформированы многопроцессорные компьютеры. Тогда появились возможности использования новых разработок не только у разработчиков операционных систем, но и у прикладных программистов.
Использование параллельных вычислительных систем (ПВС) может быть названо как одно из стратегических направлений в развитии объектов вычислительной техники. Это связано с тем, что есть определенные ограничения по быстродействию обычных последовательных ЭВМ, но при этом появляются новые задачи, при решении которых недостаточно возможностей применяемых на настоящий момент средств вычислительной техники. Задачи, связанные с синтезом антенн и дифракционных структур сложной формы, в большинстве своём подразумевают огромные объёмы математических расчётов с соответствующими требованиями к производительности используемой ЭВМ. Исходя из вышесказанного применение параллельных вычислений весьма целесообразно.
При распараллеливании вычислений основная идея связана с тем, что задача может быть поделена на совокупность меньших задач, решение которых можно проводить одновременно. При реализации параллельных вычислений обычно необходимо соблюдать координацию действий. Существуют разные виды параллельных вычислений: на уровне битов, на уровне инструкций, для данных, для задач.
При осуществлении проектирования дифракционных структур важно находить геометрические размеры конструкций, которые обеспечивают необходимые с точки зрения практики электродинамические характеристики [3, 4]. При этом одним из вопросов при проектировании является проведение выбора того, какая структура у антенны. В том случае, когда тип антенны не был заранее обозначен, то его выбор при осуществлении процессов структурной оптимизации можно сделать на основе того, что сравниваются несколько разновидностей антенн исходя из опыта проходивших до этого разработок [5, 6]. При проведении традиционного проектирования после проведения выбора типа антенны проведение ее расчёта проводится на основе метода последовательных приближений, другими словами, параметры изменяются – это размеры антенны, ее элементы (проводится параметрическая оптимизация) и сравнивают электродинамические характеристики с необходимыми [7, 8]. Для современного состояния теории антенн существуют возможности для определенных случаев не делать параметрическую оптимизацию на основе определенных процедур, сделать связь электродинамических характеристик и геометрических параметров антенн, то есть. решается задача синтеза антенн.
При решении задачи конструктивного синтеза проводится определение всей геометрии антенны, основываясь на заданных электрических характеристиках, при этом исходным параметром при решении подобной задачи рассматривается амплитудно-фазовое распределение, которое получается на базе классической задачи синтеза.
На рис. 1 изображена схема рассеяния электромагнитных волн (ЭМВ) на фрагменте объекта, состоящем из i-й и j-й полоски. Здесь Р – точка наблюдения, Q – точка – источник волны. Из рисунка видно, что изменяя угол φi, мы получаем непропорциональное ему изменение угла φj, поэтому в реализации не получится явно задавать сектор углов наблюдения. В качестве альтернативы этому можно использовать перемещение точки наблюдения по некоторому заданному отрезку SPEP с определённым шагом Δp.
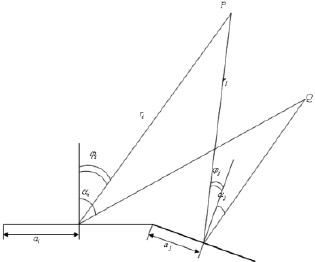
Рис. 1. Схема рассеяния ЭМВ на фрагменте объекта сложной формы
Итак, для начального момента времени задается определенный объект в виде совокупности N двумерных полосок, каждая из них характеризуется своей длиной 2a, расстоянием r до точки, в которой наблюдают, углами α и φ падения волны и расположения приемника, соответственно. Расчет характеристик рассеяния полосок проводился на основе метода краевых волн [1, 2, 9]. Помимо вышеуказанного, задается отрезок, относительно которого при вычислениях будет проходить перемещение точки наблюдения, и значение «эталонной» эффективной площади рассеяния (ЭПР), которой должен соответствовать объект, который синтезируется. Для каждой составной части такой совокупности, полоски или точки наблюдения, есть описание на основе координат в декартовых плоских системах координат. Когда изменяются координаты одной из точек по отдельной полоске должно проходить изменение частичным или полным образом величины, которые описывают эту полоску (например, когда изменяются координаты начала полоски, автоматическим образом происходит изменение таких показателей, как её длина, координат центра, углов падения и наблюдения, расстояния до точки приемника).
Реализация параллельных вычислений по k потокам происходит на основе того, что фацетная система разбивается на k частей. Есть отличие частей системы друг от друга лишь значениями отрезков наблюдения. В каждом потоке необходимо вычислять своё среднее значение ЭПР по отрезку. После того, как завершены все потоки, происходит вычисление среднего арифметического результатов – получаем искомую среднюю ЭПР по всей системе. Для каждой из итераций в алгоритме поиска средней ЭПР системы идет перемещение точки наблюдения относительно своего отрезка на некоторую малую величину Δp. Дадим запись расчётных формул по координатам точки наблюдения, которая перемещается из точки Sp по направлению точки Ep на расстояние Δp.
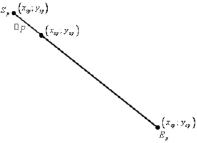
Рис. 2. Схема полоски
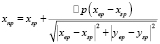 ;
;
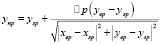 .
.
Будем считать, что ρ – является длиной отрезка наблюдения, Δp – является шагом разбиения такого отрезка, k – описывает число вычислительных потоков, n – описывает число разбиений во всей системе, ni – описывает число разбиений в i-й подсистеме (в i-м потоке), nk – описывает число разбиений в подсистеме последнего потока. Далее приведены формулы, позволяющие проводить вычисления для величин ρ, n, ni, nk.
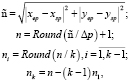
здесь Round() – является функцией округления. На рис. 3 приведена схема разбиения фацетной системы по потокам, они здесь обозначаются через ti.

Рис. 3. Разбиение системы на потоки
Для того, чтобы получить такое разбиение осуществляем такие шаги:
Создается массив из k копий по исходной фацетной системе (исходя из количества необходимых потоков).
Проводится вычисление значений величин ρ и n.
Начальную точку наблюдения выбираем в начале отрезка наблюдения первичной системы.
Для цикла по всем потокам, кроме последнего, исполняются действия:
Началом отрезка наблюдения считается то положение перемещаемой точки, в котором она была последний раз;
Перемещение точки, в которой идет наблюдение относительно отрезка первичной системы продолжается, идет расчет числа подобных перемещений до тех пор, пока это число не будет равно числу разбиений в отрезке наблюдения по текущему потоку;
Идет установление настоящего положения точки наблюдения, которое считается концом отрезка наблюдения в подсистеме фацетов в текущем потоке;
Идет перемещение точки наблюдения на величину еще одного шага.
Происходит установление текущего положения точки наблюдения как начала отрезка по которому наблюдаем фацетную подсистему в последнем потоке.
Идет вычисление величины ni, и происходит перемещение точки в сторону конца наблюдаемого отрезка в первичной системы при шаге Δp ni раз.
Делается выбор последнего положения точки наблюдения как конца наблюдаемого отрезка в подсистеме последнего потока.
Разработан параллельный алгоритм анализа объектов сложной формы, а на его основе – алгоритм нахождения геометрических форм объектов, обладающих заданными характеристиками отражения ЭМВ. Проведено тестирование производительности полученного алгоритма анализа и доказана состоятельность его использования. Выявлена зависимость успешного завершения алгоритма синтеза от значения изменения координат узлов в системе и значения точности поиска оптимальной реализации объектов.
Библиографическая ссылка
Бондаренко А.В. О РАЗРАБОТКЕ АЛГОРИТМА ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ В ЗАДАЧАХ РАДИОФИЗИКИ // Международный студенческий научный вестник. – 2017. – № 4-5. ;URL: https://eduherald.ru/ru/article/view?id=17486 (дата обращения: 27.04.2024).

