Одно из первых упоминаний о «мнимых» числах как о квадратных корнях из отрицательных чисел ученые относят к XVI веку. Итальянский инженер и математик Джироламо Кapдaнo (1501–1576) внёс значительный вклад в развитие алгебры. В 1545 году опубликовал работу, в которой, при попытке решить уравнение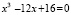 
, он получил выражение 
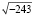. Через получившиеся выражение представлялись действительные корни уравнения: 
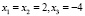. Так, в работе, Кapдaнo мнимые числа упоминались как промежуточные звенья в вычислительных действиях. Заслуга Кapдaнo заключалась в том, что он допустил существование «несуществующего» числа 
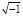, вводя правило умножения: 
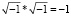. Так он первым в Европе стал использовать отрицательные корни уравнений.
Несмотря на это еще в течении нескольких сотен лет математики пытались привыкнуть к этим новым «мнимым» числам, порой предпринимая попытки избавиться от них. И только с XIX века, после публикации Карлом Фридрихом Гауссом (1777–1855) своих работ, написанных в доказательство основной теоремы алгебры, комплексные числа прижились в науке.
Вовремя расчетах цепей приходится проводить математические действия с комплексными числами, поэтому студенты инженерных направлений должны уметь выполнять следующие операции:
1) переводить комплексное число из начальной формы в необходимую;
2) находить аргумент и модуль комплексного числа и комплексное число по модулю и аргументу;
3) производить основные арифметические действия с комплексными числами [1].
Кроме того, очень важно уметь строить вектор и кривую исходя из уравнения синусоиды, вектор по комплексному числу, определять комплексное число по вектору и уравнению, уравнение по комплексному числу.
Подавляющее количество электроустановок работает на переменном токе, который изменяется по синусоидальному закону. Этим можно объяснить, почему в электротехнике тематике «Переменный ток» уделено наиважнейшее внимание [2].
Термином комплексного числа (далее в тексте – КЧ) пользуются для обозначения выражений вида: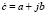 
, в которых индекс «ċ» используется для обозначения КЧ, а «а» и «b» отображают действительную и мнимую части. Значение «j» обозначает мнимую единицу и равно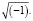 
В английском языке словом Real принято характеризовать действительность, а термином Imaginary – мнимые свойства. От этих слов были созданы обозначения Re и Im, которые используются для выражения величин «а» и «b» следующим способом:
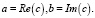
Для геометрического отображения КЧ в векторной форме применяется комплексная плоскость. У нее горизонтальная ось помечается знаком +1, а вертикальная – символом +j. Термин действительной (реже вещественной) части используется для наименования горизонтальной оси, а для вертикальной – мнимой.
Обе составляющие (действительная и мнимая) КЧ являются прямоугольными проекциями вектора на соответствующие оси.
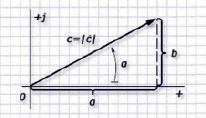
Рис. 1
В представленном графике значение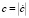 
именуется модулем КЧ и равно длине вектора. Другим параметром, определяющим положение радиус-вектора, является его угол поворота α от оси +1 до текущего положения ċ, считающийся аргументом.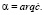 
Катеты треугольника представляются через соотношения:
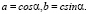
Используя тригонометрическую форму для выражения КЧ можно представить его в виде:
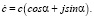
Используя формулу Эйлера ejα = cosα +
+ jbsinα, можно получить значение модуля в показательной форме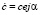 
.
В полярной форме выражение имеет вид:
.
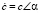Положение единичного вектора можно изобразить на комплексной плоскости:
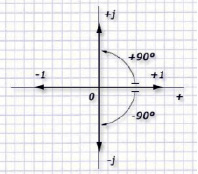
Рис. 2
Мнимая единица имеет свойства:
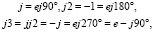
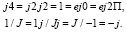
К КЧ применимо понятие сопряжения. Им называют те числа, которые равны по величине модулей и аргументов, но имеют разные знаки у аргументов.
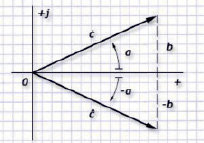
Рис. 3
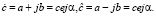
Из графика видно, что изображенные векторами КЧ симметричны по отношению к горизонтальной оси.
КЧ и математические действия. Для их сложения или вычитания делается запись в алгебраическом выражении:
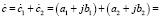
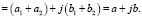
В этом соотношении отдельно суммируются мнимые и вещественные составляющие:
.
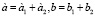Данные алгебраические сложения чисел выражают выполнение сложения соответствующих им векторов.
Выполняя сложение сопряженных чисел можно заметить, что их сумма выражается удвоенным значением вещественной составляющей:
.
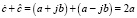Выражения КЧ в показательной форме удобны для выполнения умножения или деления. При этом у них модули перемножают или делят, значения аргументов складывают либо вычитают.
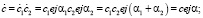
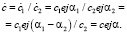
В выражении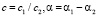 
.
Нетрудно заметить, что при действии умножения длина вектора увеличивается в величину с2, а аргумент – на значение а2. При представлении КЧ векторами соблюдается закономерность: для умножения вектора на КЧ вида aеjα достаточно растянуть вектор ва раз и довернуть на угол α.
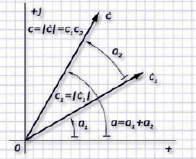
Рис. 4
Для вычисления произведения сопряженных чисел достаточно взять квадрат их модуля:
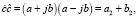
или
.
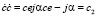Для перемножения и деления КЧ при определенных условиях удобно пользоваться их алгебраическим выражением. В таком виде действия проводятся по законам умножения многочленов и учете значения j2=-1.
.
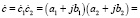
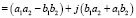Для деления чисел достаточно избавиться от значения j в выражении знаменателя методом перемножения знаменателя и числителя на одно и то же выражение сопряженного знаменателя:
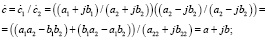
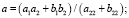
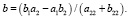
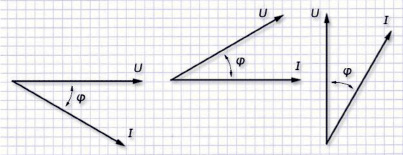
Рис. 5
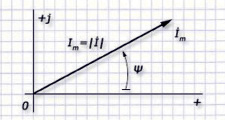
Рис. 6
Графики построенных векторных диаграмм могут иметь изображение (рис. 5):
Для выражения значения тока с синусоидальной формой пользуются соотношением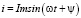 
, которым изображают на комплексной плоскости вектор с длиной Im и углом наклона ψ к горизонту. Его выражение 
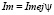считают комплексной амплитудой для тока. представляют графиком (рис. 6).
Чтобы получить действующую величину для тока требуется комплексную амплитуду разделить на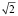 
.
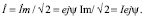
В электротехнике заглавные буквы с расположенными над ними точками (E, U, I) используются для обозначения КЧ, выражающих синусоидальные зависимости от времени ЭДС, напряжения и тока [3].
Обозначение комплексной проводимости и сопротивления делается прописными буквами Y и Z, для показа их модулей используется строчное написание у и z. Обозначение комплексной мощности выполняется символом S со значком тильда «҇» над ним.
Библиографическая ссылка
Гулай Т.А., Диговцов Г.В., Красько А.А. РАСЧЕТ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН В ЭЛЕКТРОТЕХНИКЕ С ПОМОЩЬЮ КОМПЛЕКСНЫХ ЧИСЕЛ // Международный студенческий научный вестник. – 2017. – № 4-4. ;URL: https://eduherald.ru/ru/article/view?id=17424 (дата обращения: 24.04.2024).