В математическом образовании решение задач, выступая и как цель, и как средство обучения, играют важную роль. Текстовые задачи прикладной направленности представляют собой простейший тип математического моделирования. Именно здесь формируется творческий характер использования приобретаемых математических знаний, складывается положительная мотивация изучения математики. В процессе решения задач студенты осознают, что получаемые ими математические знания не накапливаются впрок, а постоянно используются при изучении специальных дисциплин; математика – это не «тяжелый багаж», который когда-нибудь может быть пригодится, а средство формирования и повышения их профессионального мастерства.
Одной из специальных дисциплин, входящих в образовательную программу по специальности «Электрификация и автоматизация сельского хозяйства», является «Теоретические основы электротехники».
Рассмотрим пример задачи по данной дисциплине с применением основных математических моделей.
Расчёт цепи несинусоидального тока выполняется методом наложения для каждой гармоники ЭДС действующей в цепи. При расчёте можно пользоваться комплексным методом, учитывая, что индуктивное сопротивление для k-й гармоники равно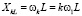 
, а ёмкостное 
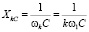[1]. Расчёт цепи для постоянной составляющей соответствует расчёту на постоянном токе, но его можно вести также как на переменном токе, полагая для реактивных сопротивлений k = 0. Тогда 
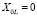, а 
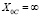. Следовательно, индуктивный элемент будет эквивалентен замыканию, а ёмкостный – разрыву цепи между точками включения [2].
Выполним в качестве примера расчёт мгновенных токов ветвей, найдем их действующие значения для цепи, изображенной на рисунке. Пусть входное напряжение равно
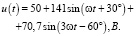
Параметры элементов цепи: R1 = 20 Ом, R2 = 5 Ом, ωL = 3Ом,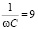 
Ом [3].
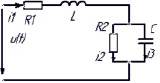
Электрическая цепь
Рассчитаем цепь от действия постоянной составляющей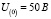 
:
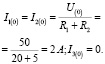
Произведем расчет параметров цепи от действия первой гармоники:
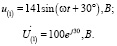
Далее найдем комплексное сопротивление параллельного участка:
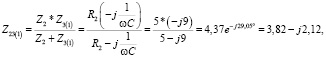Ом.
Получим эквивалентное комплексное сопротивление всей цепи для первой гармоники:
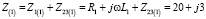
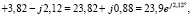Ом.
Для первой гармоники комплекс действующего значения общего тока будет равен:
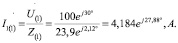
Напряжение на параллельном участке цепи:
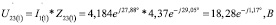
Токи во второй и третьей ветвях:
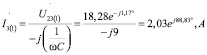
Мгновенные значения токов для первой гармоники:
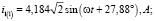
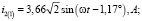
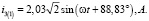
Произведем расчет параметров цепи для третьей гармоники:
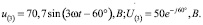
Получим комплексные сопротивления для третьей гармоники:
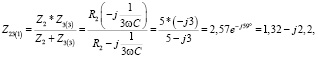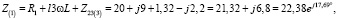Ом.
Ом.
Следующим шагом будет нахождение токов и напряжения:
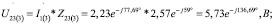
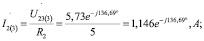
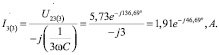
Мгновенные значения токов третьей гармоники будут равны:
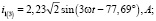
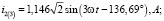
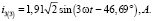
Теперь найдет значения результирующих токов в ветвях:
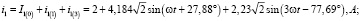
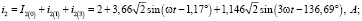
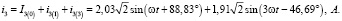
В итоге получим действующие значения токов для трех ветвей:
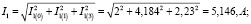
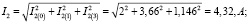
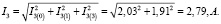
Все этапы решения данной задачи прикладного характера направлены на формирование профессионально важных качеств будущих инженеров:
- аналитического мышления;
- профессиональной компетентности;
– критического мышления.
При решении подобных текстовых задач на практических занятиях мы столкнулись с тем, что у нас недостаточно сформированы общие умения решения задач, имеются пробелы в знании физических законов. Как следствие из этого, мы испытывали затруднения в построении математической модели задачи.
Для устранения подобных проблем мы хотим рекомендовать следующее:
- решать прикладные задачи систематически, а не время от времени;
- для подготовки к решению конкретной задачи прикладного характера,
- необходимо повторение основных физических законов, применяемых в решении;
- необходимо понимать, при изучении какой специальной дисциплины и в каком разделе будет использоваться построенная математическая модель.
Таким образом, навык решения подобных прикладных задач является эффективным средством формирования профессионально важных качеств будущих инженеров.
В данной статье было показано применение метода наложения для расчета данных цепи с несинусоидальными токами. Рассмотренная нами задача может в дальнейшем являться подспорьем в нахождении данных подобных цепей [4].
Библиографическая ссылка
Гулай Т.А., Гринько А.Д., Пантелова Е.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСЧЕТА В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ С НЕСИНУСОИДАЛЬНЫМИ ТОКАМИ // Международный студенческий научный вестник. – 2017. – № 4-4. ;URL: https://eduherald.ru/ru/article/view?id=17423 (дата обращения: 19.04.2024).