Введение
Финансовый рынок является важным институтом финансовой системы современного государства, создавая условия для эффективной взаимной организованной торговли финансовыми активами и инструментами между его участниками. В современной экономической системе финансовый рынок рассматривается как механизм, позволяющий привлекать инвестиции, поддерживать экономический рост и рост благосостояния граждан [3]. В этом смысле повышение конкурентоспособности национального финансового рынка означает увеличение его возможностей в плане решения фундаментальных экономических и социальных задач.
В настоящее время многие инвесторы сталкиваются с задачей выбора активов и расчета их инвестиционных характеристик. Для этих целей используется модель теории Г. Марковица, но существуют и другие способы расчета инвестиционных характеристик [1]. В данной статье решается задача выбора оптимального портфеля активов на основании портфельной теории Г. Марковица, а так же ее модификации с помощью фундаментальных моделей доходности.
Построение оптимального портфеля ценных бумаг на основе алгоритма Г. Марковица, модифицированного фундаментальными моделями доходности.
В соответствии с моделью Г. Марковица, инвестор должен основывать свое решение по выбору портфеля исключительно на ожидаемой доходности и стандартном отклонении. Это означает, что инвестор должен оценить ожидаемую доходность и стандартное отклонение каждого портфеля, а затем выбрать "лучший" из них, основываясь на соотношении этих двух параметров [10].
В данном исследовании модель Г. Марковица модифицируется с помощью:
- коэффициента P/E (отношение цены акции к прибыли на акцию), который позволяет оценить перспективность покупки акций различных компаний для получения прибыли в будущем. Смысл коэффициента заключается в том, сколько денег инвесторы готовы платить сегодня на каждый рубль (доллар, евро) получаемой прибыли завтра [6].
- модели Гордона, которая основана на определением внутренней стоимости акции, определяемой потоком будущих дивидендов, который возрастает в течение неограниченного срока с постоянным темпом. Модель находит текущую приведенную стоимость бесконечных серий дивидендных выплат [9].
Для диверсификации портфеля были выбраны активы компаний из разных отраслей (нефтегазовая промышленность, продуктовая, строительная), входящие в список «голубые фишки»: ПAO «Лукойл», ПAO «Группа компаний ПИК», ПАО "ГМК "Норильский никель", ПAO «ВТБ», ПAO «Татнефть», ПAO «Росбанк», ПAO «Магнит».
Для нахождения инвестиционных характеристик используется временной интервал с 10.03.2016 по 10.03.2017 ежедневных цен акций на момент закрытия торгов. Источником данных для расчетов служит ресурс Investfunds [Электронный ресурс], режим доступа http://stocks.investfunds.ru/свободный. Рассчитанные значения доходностей (r) и риска приведены в таблице 1: А – по модели Марковица, В - модификация модели Марковица с помощью коэффициента Р/Е, С - по модели Гордона.
Таблица 1
Инвестиционные характеристики акций
|
A |
B |
C |
||||
|
Актив |
r, % |
Риск, % |
r, % |
Риск, % |
r, % |
Риск, % |
|
Лукойл |
14,66 |
26,34 |
31,45 |
26,34 |
62,17 |
26,34 |
|
Группа компаний ПИК |
108,28 |
34,60 |
3,07 |
34,60 |
2,08 |
34,60 |
|
Норильский Никель |
48,63 |
34,20 |
7,30 |
34,20 |
76,62 |
34,20 |
|
ВТБ |
39,70 |
37,53 |
0,09 |
37,53 |
-16,67 |
37,53 |
|
Татнефть |
18,21 |
31,78 |
15,85 |
31,78 |
16,12 |
31,78 |
|
Росбанк |
10,18 |
59,21 |
4,72 |
59,21 |
0,00 |
59,21 |
|
Магнит |
14,55 |
36,19 |
2,61 |
36,19 |
57,18 |
36,19 |
Мы наблюдаем значительные изменения доходности при переходе от одной модели к другой. В модели Марковица наибольшую доходность имеет актив «Группа компаний ПИК», при модификации модели Марковица с помощью коэффициента Р/Е – актив «ПАО Лукойл», в модели Гордона – «Норильский Никель».
Для построения оптимального портфеля для каждой имеющейся модели необходимо на график множество точек, отражающее доходности и риски портфелей [7]. Подбор долей рассчитывается с помощью таблиц в «Exсel». В качестве безрисковой ставки чаще берется доходность по облигациям федерального займа. Так как в настоящее время РФ не выпускает ОФЗ, безрисковая ставка может быть определена по средней величине доходности депозитов Сбербанка, предлагаемых к оформлению в 2017 года. Данная организация была выбрана в качестве инструмента для расчета ставки по той причине, что ей присуждена наивысшая степень надежности среди российских банков. По проделанным расчетам ставка установилась в размере 8,53%.
Для определения наиболее эффективного портфеля проведем касательную от безрисковой ставки к эффективному множеству [2]. Выбор оптимального портфеля на основе используемых нами моделей представлен на рис.1 – 3.
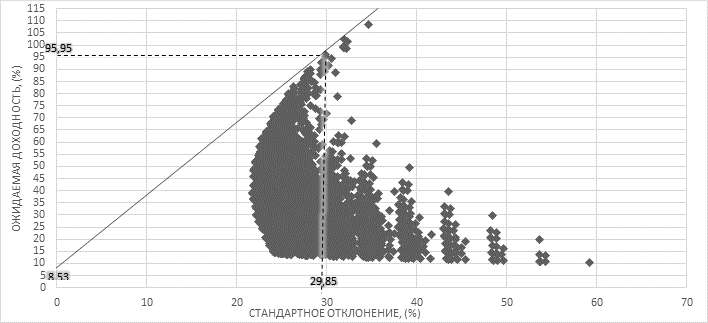
Рис. 1. Определение границы оптимального множества на основе портфельной теории Г.Марковица и У.Шарпа
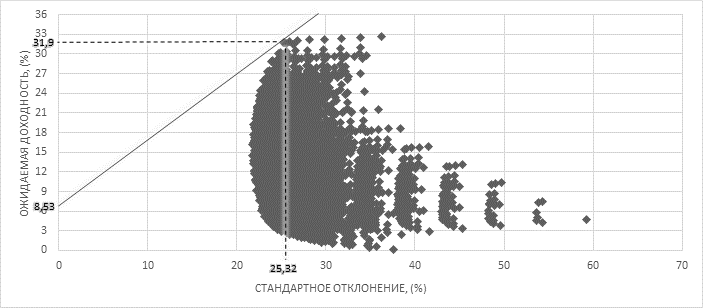
Рис. 2. Определение границы оптимального множества на основе коэффициента P/E
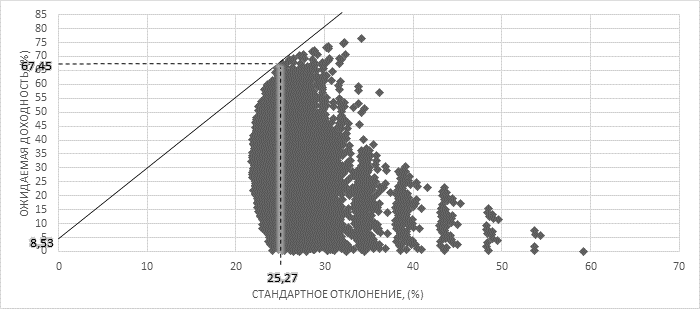
Рис. 3. Определение границы оптимального множества на основе модели Гордона
Для наглядности данные инвестиционных характеристики оптимальных портфелей приведены в таблице 2.
Таблица 2
Сравнительная таблица ожидаемой доходности и риска
|
Методики |
Доходность, (%) |
Риск, (%) |
|
Методика Г.Марковица |
95,95 |
29,85 |
|
Фундаментальная модель доходности, выраженная через коэффициент P/E |
31,9 |
25,32 |
|
Фундаментальная модель доходности, выраженная через показатели, используемые в модели Гордона |
67,45 |
25,27 |
По данным таблицы 2 видно, что наиболее привлекательными инвестиционными характеристиками обладает оптимальный портфель, построенный с помощью методики Г. Марковица. При данной модели достигается наивысшее значение доходности при низком уровне риска. Обозначим состав и структуру полученного оптимального портфеля. Доли активов в портфеле приведены в таблице 3.
Таблица 3
Состав и структура оптимальных портфелей в соответствии с классической методикой Г.Марковица и модифицированной фундаментальными моделями доходности
|
Активы |
Лукойл |
Группа компаний ПИК |
Норильский Никель |
ВТБ |
Росбанк |
Магнит |
|
Методика Г.Марковица |
0,8 |
0,2 |
||||
|
Фундаментальная модель доходности, выраженная через коэффициент P/E |
0,9 |
- |
- |
- |
- |
0,1 |
|
Фундаментальная модель доходности, выраженная через показатели. используемые в модели Гордона |
0,5 |
- |
0,4 |
- |
- |
0,1 |
Таким образом, на основе произведенных расчетов, можно сказать, что наилучшей методикой для построения оптимального портфеля является методика Г. Марковица, поскольку по результатам расчетов, доходность данного портфеля оказалась наибольшей при сопоставимом риске.
Оценка экономической эффективности предложенных рекомендаций
Для определения эффективности построенного портфеля на основе выбранной методики, рассчитаем доходность и риск портфеля индекса ММВБ.
Индекс ММВБ – взвешенный по рыночной капитализации композитный фондовый индекс, включающий 50 наиболее ликвидных акций крупнейших и динамично развивающихся российских эмитентов, виды экономической деятельности которых относятся к основным секторам экономики, представленных на Московской бирже. Рассчитывается как отношение суммарной рыночной капитализации акций, включенных в базу расчета индекса, к суммарной рыночной капитализации этих акций на начальную дату, умноженное на значение индекса на начальную дату. При расчете рыночной капитализации учитывается цена и количество соответствующих акций, свободно обращающихся на организованном рынке ценных бумаг, которым соответствует доля акционерного капитала эмитента, выражаемая значением коэффициента free-float. [4]
Free-float — ещё один показатель рынка ценных бумаг (его часто связывают с другим показателем — ликвидностью акций). Free float означает долю акций, находящихся в свободном обращении на рынке. С английского языка словосочетание free float можно перевести как «свободно плавающий». Расчет индекса производится в режиме реального времени в рублях, таким образом, значение индекса пересчитывается при совершении каждой сделки на Московской бирже с акциями, включенными в базу расчета индекса. Для расчета инвестиционных характеристик индекса ММВБ были выбраны ежедневные показатели за 2016-2017 год (с 10.03.2016 по 10.03.2017). Для сравнения показателей с оптимальным портфелем, рассчитанным и выбранным в данной работе, приведем данные в общую таблицу 4.
Таблица 4
Сравнение инвестиционных характеристик индекса ММВБ и методики Г. Марковица
|
Показатели |
Доходность, (%) |
|
Оптимальный портфель |
96,35 |
|
Индекс ММВБ |
5,63 |
Таким образом, можно сделать вывод о том, что портфель состоящий из акций ПАО «Группа Компаний Пик», ПАО "ГМК "Норильский никель", и рассчитанный с использованием методики Г.Марковица, является более привлекательным для инвесторов, чем портфель индекса ММВБ.
На основе проведенного анализа, можно дать рекомендации для инвестора. Поскольку на основе методики Г.Марковица построенный оптимальный портфель, имеет наибольший показатель фактической доходности и практически совпадает с рассчитанной ранее ожидаемой доходностью, то рекомендуется использовать именно эту методику при расчете инвестиционных характеристик оптимального портфеля.
Необходимо отметить сильные стороны данной методики. Такими являются:
· принцип полного инвестирования, т.е. портфель строится только по акциям, поэтому в нем должны отсутствовать деньги;
· отказ от игры на колебаниях, т.е. портфель ребалансируется только для поддержания оптимальных соотношения «риск-доходность» по акциям; другими словами, теория Марковица не используется для поиска точек входа и выхода из рынка;
· инвестор не использует плечо для торговли и не ведет работу по коротким позициям.
Таким образом, теория Марковица стимулирует инвесторов к владению активами и исключает игру на бирже. Эти моменты являются основным достоинством теории, которые вполне перекрывают сомнительный выбор активов по историческим данным о ценах. Слабым местом теории Марковица является ограничение, состоящее в том, что если инвестору неизвестно математическое ожидание и стандартное отклонение по ценным бумагам, то он соглашается с тем, что оценить эти величины можно будет в будущем на основании имеющихся исторических данных. Однако в зависимости от глубины исторических данных можно получить совершенно разные результаты для анализа [5].
Заключение
В целом любые модели инвестиционного портфеля являются открытыми системами и соответственно могут дополняться и корректироваться при изменениях условий на финансовом рынке. Модель инвестиционного портфеля позволяет получить аналитический материал, необходимый для принятия оптимального решения в процессе инвестиционной деятельности [8].
Основным выводом данной работы является то, что при расчете инвестиционных характеристик по методике Г. Марковица фактическая доходность портфеля наибольшая, именно поэтому рекомендуется при расчете оптимального портфеля использовать данный подход.
Использование компьютерной реализации моделей значительно увеличивает оперативность получения аналитического материала для принятия решения. Тем самым выполняются такие основные свойства управления как: эффективность, непрерывность и оперативность.
Библиографическая ссылка
Кабанова А.Е. ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ ПО АЛГОРИТМУ Г. МАРКОВИЦА, МОДИФИЦИРОВАННОГО ФУНДАМЕНТАЛЬНЫМИ МОДЕЛЯМИ ДОХОДНОСТИ ЦЕННЫХ БУМАГ // Международный студенческий научный вестник. – 2017. – № 3. ;URL: https://eduherald.ru/ru/article/view?id=17223 (дата обращения: 26.04.2024).

