Задачи на смеси, сплавы и проценты всегда вызывали сложности у учащихся. Статистические данные по анализу результатов ЕГЭ по математике показывают, что решаемость задания, содержащего текстовую задачу, приблизительно равна 30%. Хотя основным видом учебной деятельности, в ходе которой происходит усвоение системы математических умений, знаний и навыков, принято считать решение задач, так как они являются средством, направляющим и стимулирующим учебно-познавательную деятельность [4].
Трудности при решении сюжетно-текстовых задач, в частности задач на проценты, объясняются в значительной степени тем, что помимо технического аппарата, который применяется алгоритмизировано, требуется ещё и этап, на котором составляется уравнение (система уравнений) и требуется осознание имеющихся условий задачи и их перевод на язык математики.
Различают несколько подходов к определению самой задачи. Л.М. Фридман считает, что задача – это вопрос (требование), ответ на который можно найти отталкиваясь от условий этой задачи [1].
Роль текстовых задач в процессе обучения математике многообразна. Множество их функций наиболее всесторонне охарактеризовал Е.С. Ляпин. Он говорил, что при решении задач происходит формирование различных математических понятий, а также осмысление различных арифметических операций. Чаще всего задачи являются основой для вывода некоторых теоретических положений, способствуют обогащению и развитию правильной речи учащихся, помогают учащимся понять количественные соотношения различных жизненных фактов, содействуют воспитанию учащихся и развитию их логического мышления [2].
Задачи на растворы, смеси и сплавы занимают особое место среди текстовых задач. Особо важным является то, что в структуре различных проверочных работ по математике они относятся к заданиям повышенного уровня сложности. Некоторые учащиеся, увидев такую задачу, отказываются ее решать, и это логично, ведь в учебниках их мало, а в вариантах самостоятельных, контрольных, экзаменационных работ они есть. Также можно отметить и тот факт, что немногие могут самостоятельно справиться с подобного рода задачами. Проанализировав учебники, можно сказать, что вся теория по решению таких задач заключается в учебниках 5-6 классов.
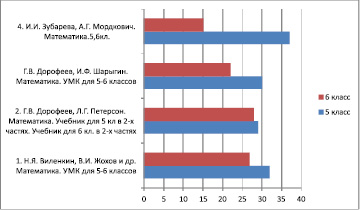
Далее приведено сравнение учебников математики 5-6 классов на наличие сюжетных задач (их количество).
Можно отметить, что количество таких задач в учебниках авторов Н.Я. Виленкина, В.И. Жохова и Г.В. Дорофеева, Л.Г. Петерсона значительно больше, чем в остальных представленных учебниках.
Для того, чтобы хоть как то увеличить количество задач на растворы, смеси и сплавы и как можно лучше закрепить схемы их решений в памяти учащихся, разрабатываются частные методики, а так же конспекты интегрированных уроков математики и химии, тем самым ещё раз подчеркивая межпредметные связи.
Решение задач на смеси, сплавы, растворы требует определенной теоретической базы. Это различные определения, такие как концентрация, процентное содержание и др., а также и всевозможные допущения, например:
1) всё, что мы рассматриваем, считается однородным;
2) все процессы происходят мгновенно;
3) полученное вещество состоит из смешиваемых веществ и равно сумме их объемов;
4) величины, получаемые в результате вычислений, не могут быть со знаком минус.
Существует несколько способов решения задач на слияние растворов. Например, можно воспользоваться расчетной формулой, как это делают на уроках химии. Из области математики можно пользоваться графическим или же алгебраическим методами. Более простым в применении является метод, в котором указанные задачи решают по «правилу креста». К сожалению не каждый преподаватель знает о нем и применяет его на практике.
Подробно методы решения подобных задач описаны в работе Е.С. Ежовой [3].
Проведенное нами исследование современных школьных учебников, методической литературы по проблеме обучения учащихся решению задач на смеси и сплавы позволяет констатировать следующее. В школьных учебниках недостаточно теоретического и практического материала, который позволил бы учащимся приобрести умения и навыки в решении указанных задач, а тем более для того, чтобы решать эти задачи на экзамене. Поэтому учителю приходится самостоятельно не только подбирать нужную информацию из каких-либо других источников, но и разрабатывать соответствующий методический инструментарий, а также продумывать методы обучения школьников решению задач на смеси и сплавы.
Библиографическая ссылка
Кузнецова Ю.И., Дворникова Ю.Е. ЗАДАЧИ НА СМЕСИ И СПЛАВЫ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ // Международный студенческий научный вестник. – 2016. – № 5-3. ;URL: https://eduherald.ru/ru/article/view?id=15937 (дата обращения: 20.04.2024).

