В математическом анализе немаловажное место занимает логарифмическое дифференцирование. В данной статье мы постараемся выявить взаимосвязь экономического процесса и логарифмического дифференцирования, как метода математического анализа. Логарифмическое дифференцирование является наиболее оптимальным математическим методом для экономического анализа, в тех случаях, когда необходимо преобразовать функцию, выражающую зависимость между стоимостью общих затрат на производство и стоимостью выпускаемой продукции. Формированию дифференциального исчисления как прикладного, а позднее и научного метода, предшествовало появление стройной философской теории, созданной Николаем Кузанским.
Также существенный вклад в развитие основ дифференциального исчисления внесли французские ученые П. Ферма (1601 – 1665) и Р. Декарт (1596 – 1650), а в XVII веке И. Ньютон пришел к понятию производной, решая задачи механики, связанные с нахождением мгновенной скорости.
Основываясь на том, что потребитель должен поступать рационально, экономист определяет оптимальное соотношение изменений благ и издержек, при котором данные предельные величины равны. Основной задачей, как микро, так и макроэкономики являются выявление таких закономерностей и зависимостей, разработка наилучшего плана действий и другое.
Чтобы понять роль логарифмического дифференцирования, для начала рассмотрим такое понятие как дифференцирование. В математике дифференцированием называется процесс нахождения производной. Но иногда возникают ситуации, когда процесс нахождения производной достаточно сложен. Чтобы его облегчить сложные функции предварительно логарифмируют, в этом и заключается суть логарифмического дифференцирования. Данный метод является наиболее оптимальным при нахождении производной произведения нескольких функций или их участки, а также при дифференцировании выражений, имеющие корни из дробей (функций),
Рассмотрим метод более детально. Пусть дана функция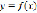 
. Прологарифмируем правую и левую часть.
Получим: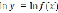 
Затем продифференцируем данное выражение как сложную функцию, с учетом того, что y – это функция от x
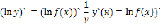
В результате искомая производная равна
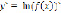
Производная такого вида называется логарифмической, а процесс её нахождения логарифмическим дифференцированием. Рассмотрим конкретный пример. Необходимо найти производную функции
.
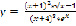Прологарифмировав правую и левую часть, получаем
;
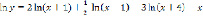Дифференцируем данное выражение
,
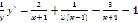отсюда получаем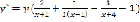 
В некоторых функциях, например как степенно-показательных, производная вычисляется только методом логарифмического дифференцирования. Данный метод также применяется для вычисления в тех случаях, когда аналитическое выражение функции включает несколько множителей.
Как говорилось ранее, логарифмическое дифференцирование имеет экономический смысл. Заключается он в том, что производительность труда есть производная объема произведенной продукции по времени. Иными словами, производная логарифмической функции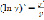 
, где 
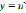обозначается логарифмической производной, или же относительной скоростью изменений функции или темпом изменения функции. Если данный темп будет положительным, то скорость изменения увеличивается, если же отрицательным, то скорость сокращается.
Рассмотрим это на примере. Производительность труда рабочих предприятия может быть задана следующим уравнением
, 
,
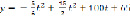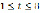где t – рабочее время в часах.
Необходимо вычислить темп и скорость изменения производительности труда через полтора часа после начала работы и за полчаса до ее начала, при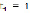 
, 
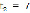
Производная выражает производительность труда
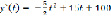, а темп изменения производительности и скорость – соответственно производно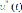й 
и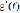 
и логарифмической производной 
.
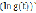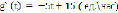
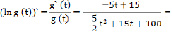
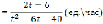
Если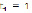 
, то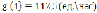
;
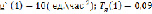
Если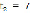 
, то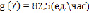 
;
; 
;
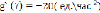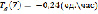Очевидно, что в конце рабочего дня производительность труда резко снижается, а изменение с положительного знака на отрицательный означает то, что возрастание производительности труда в начале рабочего дня сменяется ее уменьшением в последние часы.
Подводя итог, можно сказать, что логарифмическое дифференцирование играет очень важную роль, как в математическом анализе, так и в исследовании различных экономических явлений и процессов.
Библиографическая ссылка
Цыплакова О.Н., Васильева В.А. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ В ЭКОНОМИЧЕСКИХ ПРОЦЕССАХ // Международный студенческий научный вестник. – 2015. – № 3-4. ;URL: https://eduherald.ru/ru/article/view?id=14143 (дата обращения: 21.11.2024).