Оценка напряженного состояния не может быть корректно выполнена без установления зависимости между условными напряжениями и деформациями. Для этого применяются различные зависимости. Наиболее широкое распространение получила упрощенная идеализированная прямолинейная диаграмма работы материала (диаграмма Прандтля). Ее использование привело к появлению различных практических методов расчета элементов, избавив от необходимости рассмотрения различных диаграмм для каждого из материалов, и позволило разработать общие методы расчета конструкций из различных металлов. На ней пределы пропорциональности и текучести и соответствующие им условные деформации принимаются равными 1. Данная диаграмма четко разграничивает упругую и упруго-пластическую стадии работы материала конструкции.
В последнее время предпринимаются различные попытки применения диаграмм с криволинейными участками между пределами пропорциональности и текучести. Среди них следует отметить экспоненциальную кривую и кривую с эллиптическим участком.
Мы попытались сравнить деформации и прогибы элементов коробчатого сечения (рис.1 а) для диаграммы Прандтля и эллиптической в процессе исчерпания несущей способности из-за двухсторонней текучести материала (рис. 1 б, в).
Общепринято [1] задавать линию оси деформированного стержня в виде полуволны синусоиды. Мы, по аналогии с [2, 3], для вычисления прогибов стержня использовали обычные интегралы Мора, полагая прогиб fx на расстоянии z от опоры равным
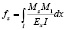, (1)
где Mz – момент от силы N; M1 – момент от единичной силы, приложенной в точке определения прогиба (на расстоянии z от левой опоры); I – осевой момент инерции сечения стержня; Ex – приведенный условный модуль, изменяющийся по длине зоны пластического деформирования.
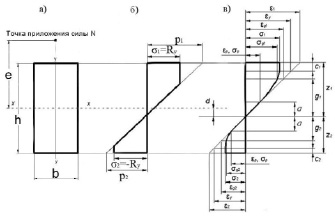
Рис. 1. Эпюры напряжений и деформаций: а – сечение; б – при диаграмме Прандтля; в – при эллиптической диаграмме
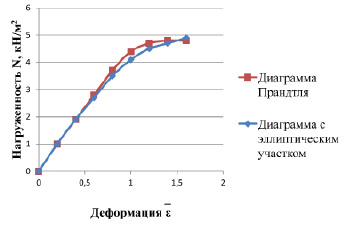
Рис. 2. Диаграмма деформаций сжатого пояса в среднем сечении
Для вычисления прогибов, напряжений и деформаций разработан следующий алгоритм, реализованный в [4]:
1. Производится ввод исходных данных – размеры стержня и сечения, нагрузка и эксцентриситет ее приложения, расчетное сопротивление стали.
2. В первом приближении вычисляются балочные упругие прогибы в 99 точках стержня.
3. Определяем моменты внешних сил в 101 точке (включая опоры).
4. Для каждого отрезка вычисляем напряжения и значения модуля Ех.
5. Находим прогибы, учитывая новые модули деформаций.
6. С полученными значениями прогибов программа возвращается к пункту 3 алгоритма, до обеспечения заданной точности расчетных значений.
7. Остаточные прогибы вычисляются после полной разгрузки стержня.
8. Исходные данные и полученные величины прогибов и деформаций выводятся на печать.
В результате расчетов по различным диаграммам работы материала были определены значения в точках на опорах и в точках расположенных на расстояниях 0,1l по длине стержня. Результаты расчета показали, что при упругой работе материала деформации и прогибы практически не зависят от вида диаграммы работы материала и формы изогнутой оси (рис. 2). По мере роста нагрузки при деформациях превышающих предел пропорциональности диаграммы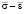 
расходятся все сильнее с ростом высоты сечения и соотношения площадей полок и стенок. Использование идеализированной диаграммы приводит к значительному занижению перемещений стержня. Предельные нагрузки достаточно близки для обоих видов диаграмм.
Библиографическая ссылка
Селезнев А.Д., Петрова О.А., Буланов В.Е. К ВОПРОСУ ОЦЕНКИ НАПРЯЖЕННО ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ВНЕЦЕНТРЕННО-СЖАТЫХ ЭЛЕМЕНТОВ // Международный студенческий научный вестник. – 2015. – № 3-1. ;URL: https://eduherald.ru/ru/article/view?id=12094 (дата обращения: 24.04.2024).