Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

• Авторы
• Файлы
• Литература

Курносов В.Е. 1 Андреева Т.В. 1 Назиров Р.Р. 1 Хиля Д.Е. 1

---

1 Пензенский государственный технологический университет

Статья в формате PDF

2537 KB

1. Андреева Т.В. Программный комплекс исследования динамики пластинчатых конструкций электронной аппаратуры в широком частотном диапазоне на основе дискретно-непрерывной модели / Т.В. Андреева, В.Е. Курносов // ХХI век: итоги прошлого и проблемы настоящего плюс: Периодическое научное издание. – Пенза: Изд-во Пенз. гос. технол. ун-та, 2013. – № 10(14). С 215 – 221.

2. Курносов В.Е. Логико-математические модели в задачах проектирования электронной аппаратуры и приборов: Монография / В.Е. Курносов, В.И. Волчихин, В.Г. Покровский. – Пенза: Изд-во Пенз. гос. технол. ун-та, 2014. – 148 С.

3. Бидерман В. Л. Механика тонкостенных конструкций. Статика. – М.: Машиностроение, 1977. – 488 с.

Использование дискретно-непрерывных методов решения задач при проектировании изделий позволяет получить существенный положительный эффект [1, 2]. Разрабатывается система моделирования динамики узлов на печатных платах с расширенными функциональными возможностями, позволяющая исследовать в широком частотном диапазоне реакцию конструкции при произвольном заданном воздействии.

Основное уравнение с учетом потерь энергии на внутреннее трение:

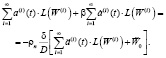(1)

Здесь b – коэффициент вязкости материала пластины; D – цилиндрическая жесткость; E – модуль Юнга; n - коэффициент Пуассона; 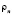 – приведенная плотность материала с учетом массы навесных элементов, функция координат; d – толщина пластины;  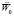– задаваемое воздействие;  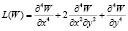– дифференциальный оператор. Выражение для прогиба имеет вид

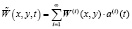, (2)

где 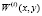– собственные формы; 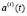– функции времени, подлежащие определению.

Функция 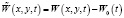является характеристикой прогиба, необходима для определения сил инерции. С учетом ортогональности собственных форм получим систему несвязанных уравнений:

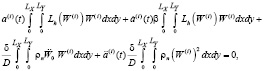(3)

где 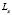, 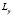– размеры пластины. В уравнениях вида (3) дифференциальный оператор 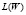заменен разностным 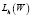. для нахождения функций 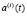, , 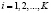имеем 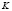неоднородных дифференциальных уравнений (4) второго порядка, которые приведем к виду:

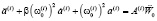. (4)

Здесь 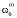 – собственные частоты,  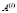– масштабные коэффициенты. Воздействие произвольного вида 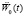можно аппроксимировать ступенчатой функцией, задаваемой отсчетами, полученными через равные интервалы времени.

На рисунке показаны нормированные собственные формы, соответствующие характеру движения платы на 1-й, 2-й, и 11-й собственных частотах.

Собственные формы и частоты колебаний прямоугольной пластины

Использование дискретнонепрерывных моделей при разработке узлов на печатных платах позволяет исследовать локальные резонансные явления и влияние внешних механических воздействий в широком диапазоне частот, обеспечивать при проектировании устойчивость конструкций к ударным и вибрационным воздействиям.

Библиографическая ссылка